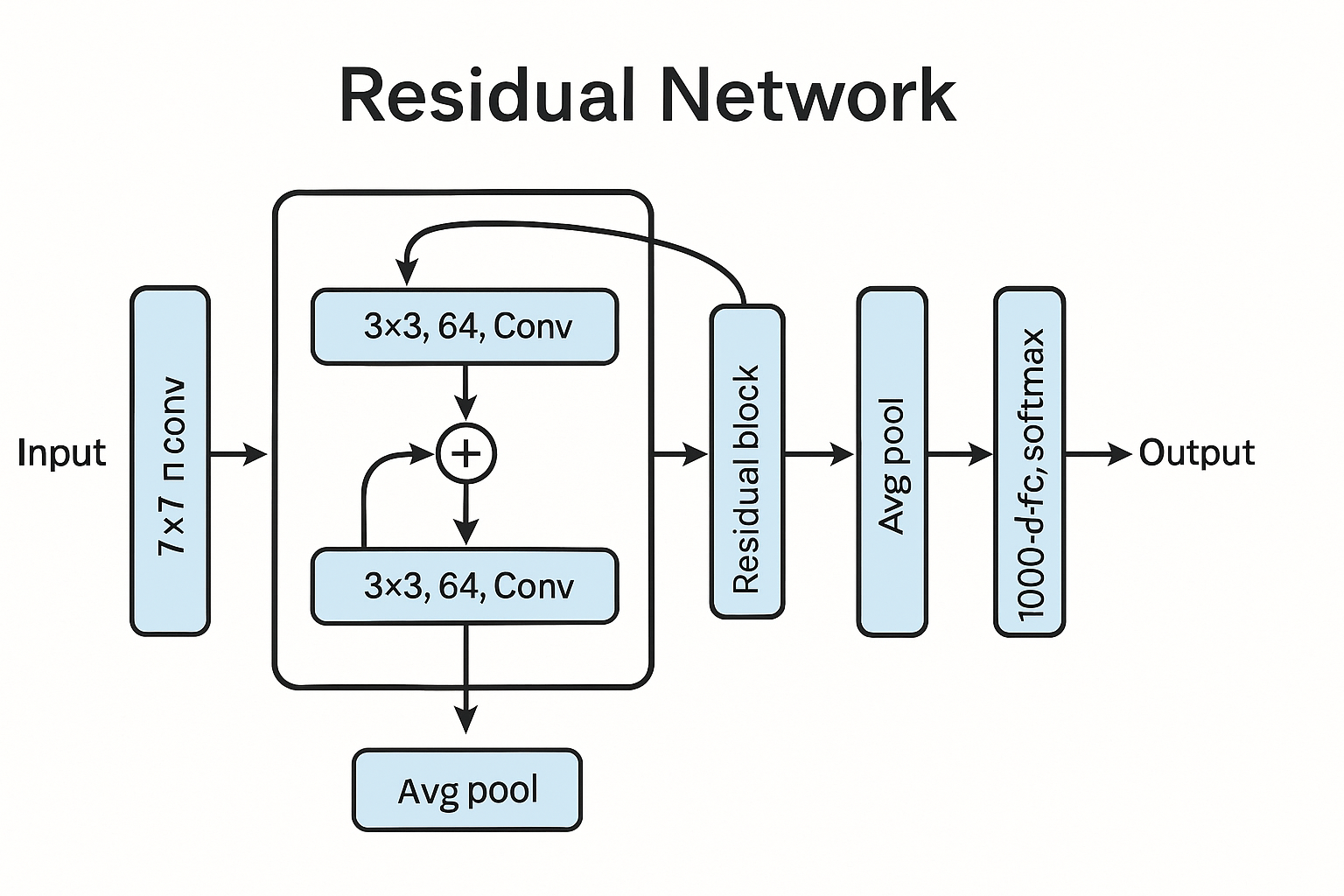
Deep Residual Learning for Image Recognition

第一遍阅读

作者

作者我就知道何恺明和孙剑, 当时发表的时候四人还不算有名
单位是 MSRA, 微软亚洲研究院, 当年是为数不多的纯粹做研究的研究院. 其中另外两人应该是当时的实习生

摘要

深的神经网络难以训练. 使用残差学习框架的网络能够优化训练, 使得更加容易
用中间层去训练残差方程, 而不是没有参照的方程
增加层数后, 有很好的效果

对于 ImageNet 数据集, 采用 152 层, 比当时的 VGG 都多了八倍.
当时 Google 的 Googlenet 也同期推出, 但并不是很深, 而是很宽
有更低的复杂度, 更好的效果 – 赢下了 ImageNet 的竞赛

对很多网络, 深度很重要
仅仅把原先的网络换成残差网络, 就得到了大幅的提升

这篇文章并没有结论.
CVPR限制最多八页, 由于要放许多实验结果, 因此没地方放结论了

图片

原始网络训练效果

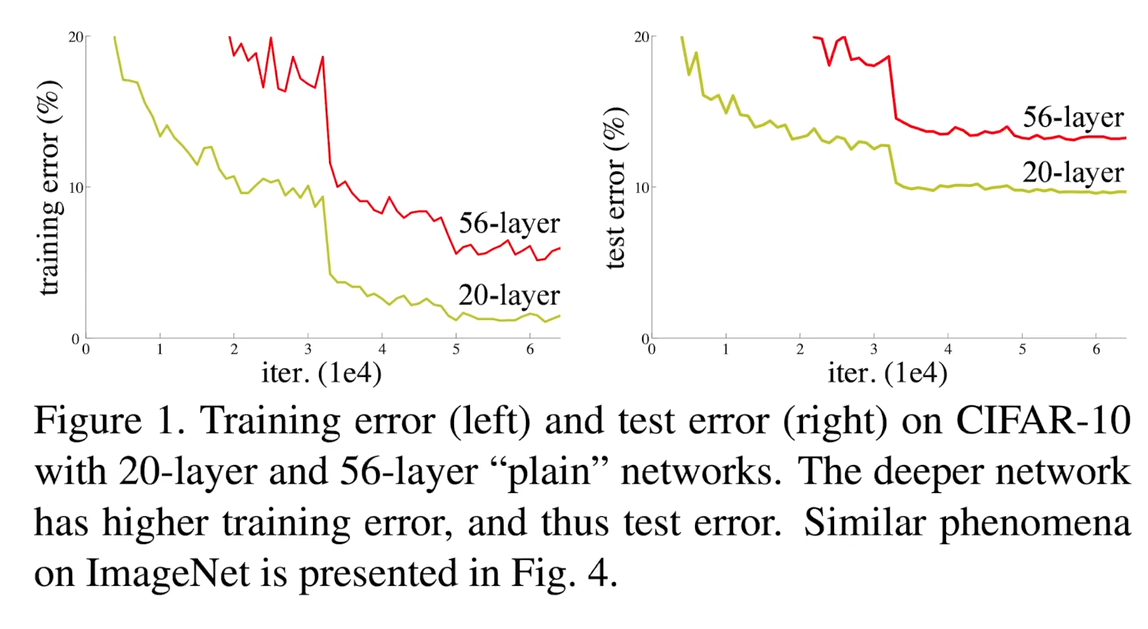
../../source/ResNet插图.png
这张图展现了对于普通神经网络, 训练更深的神经网络会导致更差的效果
不仅是过拟合的问题, 就算在训练集上的误差也很大

残差块

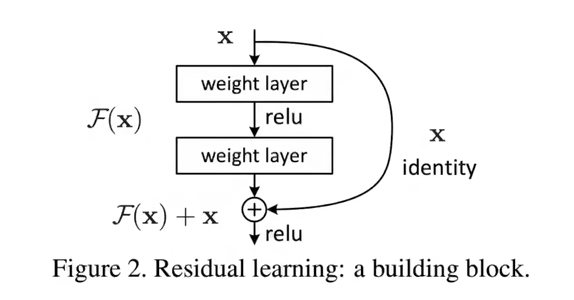
$../../source/ResNet\_2.png$
后面细说

残差网络的效果

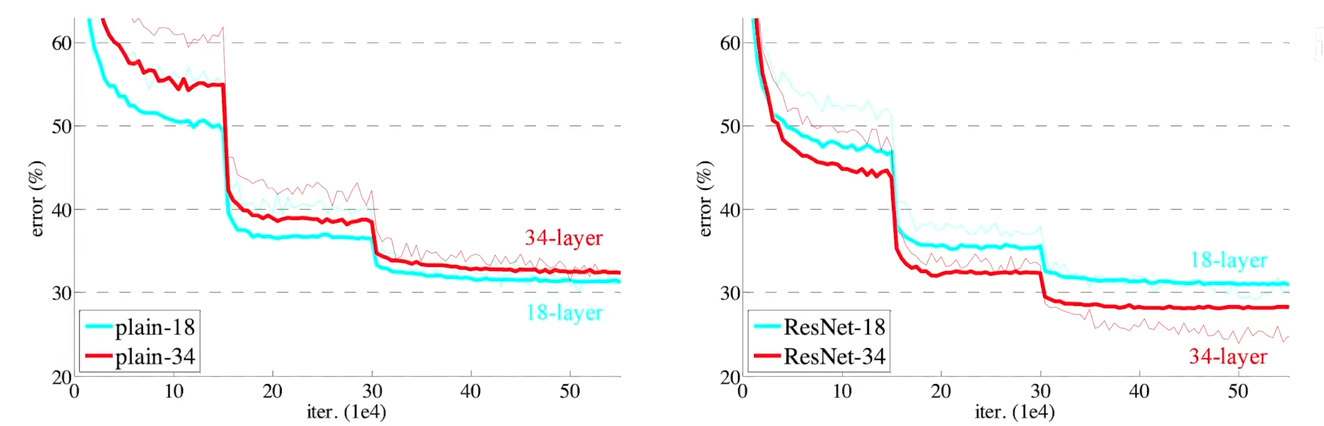
$../../source/ResNet\_3.png$
在没使用残差的时候, 34 层的网络效果不如 18 层
使用残差后, 34 层的效果明显好于 18 层

数据表格

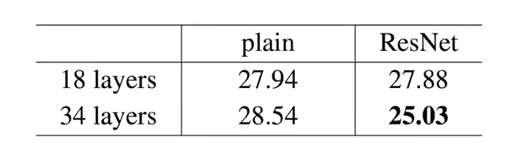
$../../source/ResNet\_4.png$
虽然图像更加直观, 但是表格包含的数据同样重要
比如, 后面的引用者, 可以更加方便的对比数据, 使用数据

第二遍阅读

导言

深度卷积神经网络好, 因为可以通过增加层数提升网络深度. 不同的层可以学到不同级别的特征

网络深度的困境

提出问题:

难道学好一个网络, 只是简简单单的增加网络深度吗?

然而现实情况是, 随着网络层数加深, 会面临梯度爆炸/消失.
为了解决梯度的问题, 可以使用一些方法:

较好地初始化, 避免极端数据的影响
进行批量归一化, 层归一化, 使得收敛
然而, 即使能训练了, 网络变深之后, 精读也会变差(可以看开始的那张图)
这并不是因为过拟合, 而是训练误差本身就变高了

无法学到恒等映射

对于同一个网络, 对于那些更深的, 即使把多出的那些层学成恒等映射, 也就是 f(x)=x, 也至少能做到和浅的网络相等
然而, 现实情况是, 学成恒等映射是一个比较困难的事, 因此导致了深度增加后的精度下降

学习残差

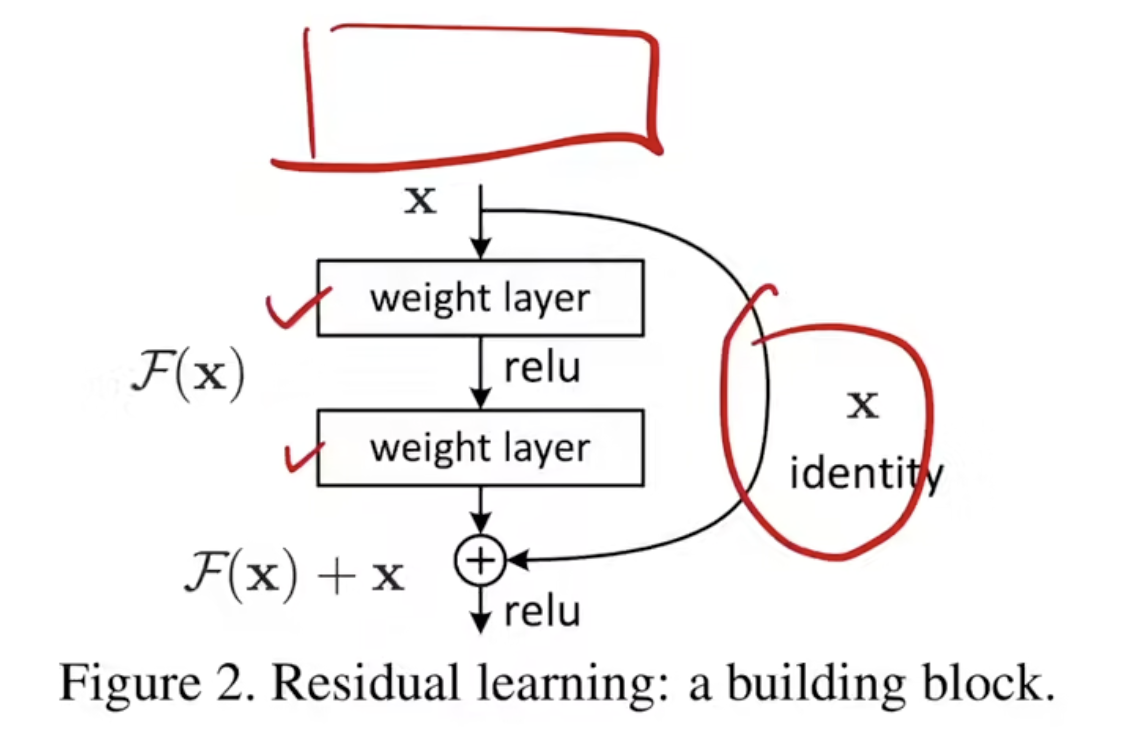
$../../source/论文精读 ResNet\_残差块.png$
这里$F(x)$函数不再是学习一个函数$H(x)$, 而是学习一个残差函数:$F(x) = H(x)-x$, 并把这个函数与 x 相加
虽然多了一个把之前学到的 x 进行相加的过程, 但是并没有改变参数, 因此不会提升模型复杂度以及计算复杂度

具体实现

处理输入输出的通道数

由于残差块中需要把输入输出进行相加,得到最终的输出, 因此需要保证二者的通道数相同
文章中提供了一些方法:

添加一些额外的零, 使得通道数相等
使用 1x1 卷积层, 不影响空间维度, 在通道数上做出改变

图片处理

在训练和测试中, 使用了多种尺寸的图片, 且图片也是随机采样而得
这个在刷榜中比较常见, 不过在真实场景中, 一般不会为了一点点的提升而增加巨大的成本

实验

bottleneck

对于层数较多的 resnet, 作者引入了一个叫做 bottleneck 的设计:
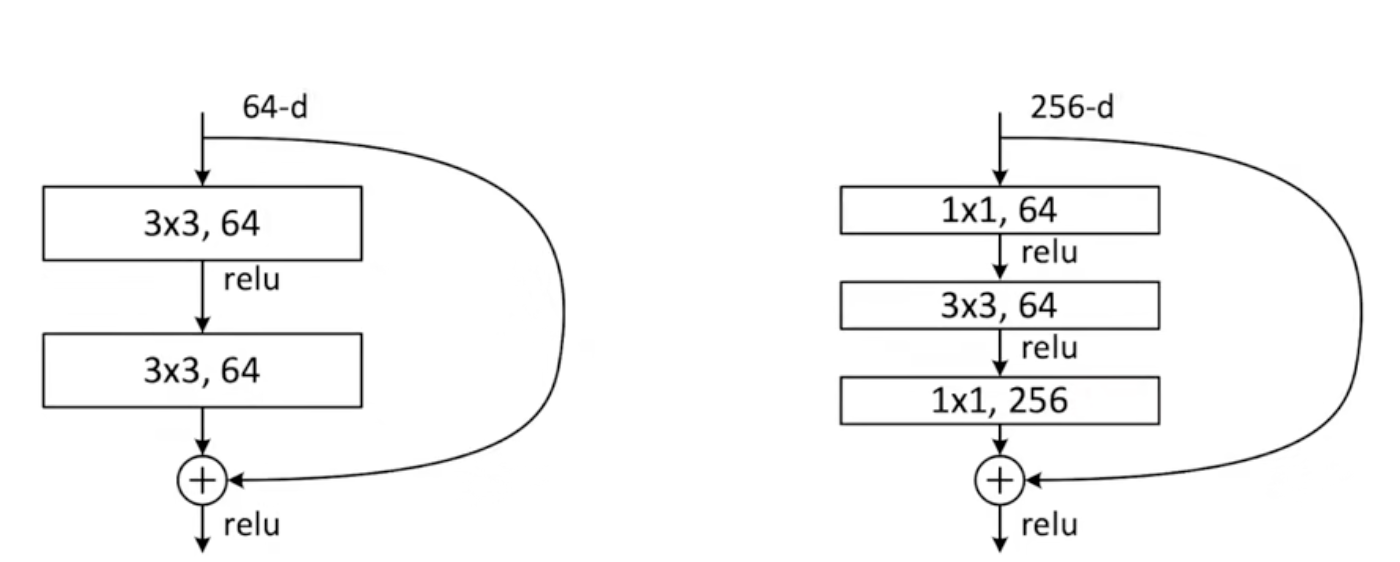
$../../source/论文精读 ResNet\_bottleneck.png$
左侧是常规的残差块, 右侧是 bottleneck 设计的残差块
这里对于通道数先进行了降维, 从 256 到 64, 再进行特征提取后, 再利用 1x1 进行通道数升维, 完成相加
虽然在通道数的变换, 降维中损失了一些精读, 但是却减少了算法的复杂度, 提升了效率, 实现了和左侧接近的复杂度

理论层面

残差结构梯度求导（ResNet）

链式法则

$$ \frac{\partial f(g(x))}{\partial x} = \frac{\partial f(g(x))}{\partial g(x)} \cdot \frac{\partial g(x)}{\partial x} $$

残差结构的求导

$$ \frac{\partial [f(g(x)) + g(x)]}{\partial x} = \frac{\partial f(g(x))}{\partial x} + \frac{\partial g(x)}{\partial x} $$

其中第一项继续用链式法则展开：$$
\frac{\partial f(g(x))}{\partial x} = \frac{\partial f(g(x))}{\partial g(x)} \cdot \frac{\partial g(x)}{\partial x}

$$
$$
第二项是捷径分支（shortcut）的直接梯度。

总结

残差结构的梯度 = 主分支梯度 + 捷径梯度
这样设计有助于缓解深层网络中的梯度消失问题，是 ResNet 能训练很深的核心原因。
主分支梯度由于函数的嵌套, 其实比较小, 这里的主导项是后面的捷径梯度. 正是这一项让残差结构的梯度更大, 即使在较深的网络中也能训练的动

【论文精读】 ResNet