在发小的推荐下, (重新)学习一下信息论, 希望能为 ai, llm 等领域的学习打下一个更坚实的基础
其实大一上就上过信通概论, 当时大家都说是水课, 我也懒得听, 便听了两节就不去了
现在回过头看似乎还是有些有用的东西的, 虽然确实水
我选择跟随 MIT 6.050J 信息论课程的 notes 部分, 配合 gpt 的讲解, 来完成信息论的学习
Information and Entropy | Electrical Engineering and Computer Science | MIT OpenCourseWare
1.0 比特 Bits
信息的单位: 比特 Bits
- 比特是信息量的度量单位
- 这里强调的是信息量, 是数量而非内容和含义
信息的度量方式
- 物理学中, 用焦耳/开尔文(J/K) 来度量信息
- 和热力学的熵相关
- 信息论中, 最常用的度量是比特 bits
如何量化信息
- 不确定性的消除程度
举例:
- 抛一枚公平硬币 → 2 个可能结果
- 如果 Alice 想告诉 Bob 抛硬币的结果,只需传递“1 比特”
- 抽一张扑克牌 → 52 种可能结果
- 要告诉 Bob 抽到的是哪一张牌,就需要更多的信息量
计算:
如果有 N 个等可能的结果, 则所需要的信息量是:
这里是针对等可能的结果, 对于不等可能, 后面应该会讲到, 要用的"自信息" 这一概念
通信过程
1. 建立编码规则
- 通信双方会约定好编码(code), 比如哪个编号对应哪种情况
2. 发送数据
- 一方根据现实情况, 根据规则传送编号
- 另一方根据规则, 接受并理解信息
不确定性与信息量
- 一方发消息前, 另一方对结果不确定(缺少信息)
- 发送比特后, 另一方的不确定性减少
- 因此:信息量 = 不确定性减少的量
- 在 1 阶段,Bob 甚至因为知道“有信息将要传来”,不确定性反而增加了
- 在 2 阶段,不确定性被减少
详细过程
- Setup 阶段:
- 不确定性增加(Bob 从“什么都没想过” → “知道有未知”)
- 信息量并没有减少,因为没有“确定性”增加
- Outcome 阶段:
- 不确定性减少,才真正等于获得了信息量
1.1 布尔比特 Boolean Bit
为什么只用 0 和 1
- 计算机世界使用二进制
- 这是物理系统中最容易实现的两个稳定状态
- 把表示方式抽象成 0,1 后, 不需要关心具体内容, 只需要关心形式规则
一元布尔输入(单输入)
输入 $x∈{0,1}$,输出也只能是 0 或 1。总共有 4 种可能的函数:
| 输入 | 恒等 (Identity) | 非 (NOT) | 恒 0 (ZERO) | 恒 1 (ONE) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
- 恒等: 输出=输入
- 非: 取反
- 恒 0/恒 1: 和输入无关, 直接给定
二元布尔输入(双输入)
输入 $A,B∈{0,1}$,共有 22=422=4 种输入模式(00, 01, 10, 11)。
-
每种模式的输出可以独立设为 0 或 1 → 一共有 $2^4=16$ 种可能的函数
-
AND(与):只有当 A=1 且 B=1 时才输出 1
-
OR(或):只要 A 或 B 有一个是 1,就输出 1
-
XOR(异或):当 A 和 B 不一样时输出 1
-
NAND(与非):先做 AND, 再取反
-
NOR(或非):先做 OR, 再取反
以下是针对四种双输入的运算表格
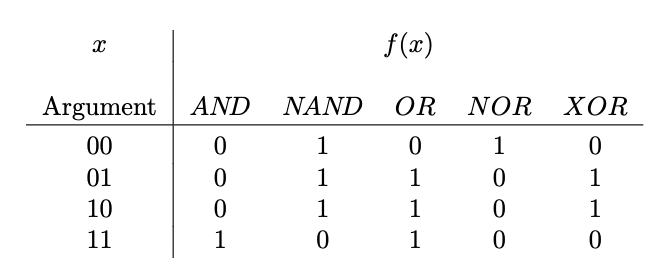
布尔代数运算符
这是一些逻辑运算符

注意这里不要把 OR 运算中的+符号与整数加法混淆
布尔代数定律
以下等式对所有布尔变量都成立
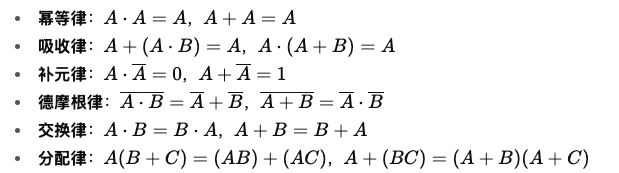
可以用于电路简化, 逻辑推理, 代数证明
可逆性
- 一元函数里:恒等和取反是可逆的(输入 ↔ 输出一一对应)
- 二元函数:一般是不可逆的(因为输入 2 位 → 输出 1 位,丢信息)
- 但组合函数可以是可逆的,比如:
- 输出 = (A⊕B, A),这是 2 输入 → 2 输出,可逆
延伸:这和 量子计算有关,量子演化必须可逆(幺正运算)
1.2 电路比特 Circuit Bit
从布尔表达式到逻辑电路
- 在 布尔代数 中,我们写的是公式(如 A⋅B+C‾A⋅B+C)
- 在 电路 中,每个布尔函数对应一个逻辑门(gate):
- NOT → 反相器
- AND → 与门
- OR → 或门
- XOR → 异或门
- NAND / NOR → 与非 / 或非门
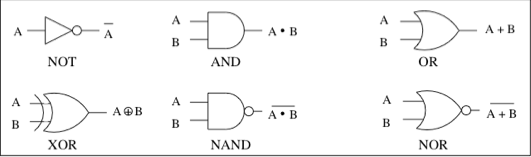
组合逻辑
- 定义:输出只依赖于当前输入,没有“记忆”
- 特点:
- 电路里没有反馈环路(no loops)
- 输入确定 → 输出立即确定
- 用真值表或布尔表达式就能完整描述
电路比特的特点
- 可以复制:一个门的输出可以接到多个门的输入
- 可以丢弃:如果某个输出不用,就留空即可
- 这和布尔比特完全一致,也是为什么 电路比特是布尔比特的物理实现模型
1.3 控制比特 Control Bit
程序中的布尔条件
- 在计算机程序里,布尔表达式通常用来控制执行流程
- 典型的例子就是
if语句 - 控制比特(control bit) = 程序里的“条件判断”信号
控制比特与布尔代数的区别
控制表达式的语义 ≠ 纯粹的布尔代数
- 在布尔代数里,我们总是“完整计算”表达式的值
- 在程序控制里,有个优化:短路求值 (short-circuit evaluation)
例子
- 表达式
(and (< x 0) (> y 0)):- 如果先算
x<0,发现为假,那么整个 AND 就是 0,后面的y>0根本不用算 - 程序直接跳过,节省运算时间,还避免可能的副作用(例如
y>0判断里如果有函数调用就不会执行)
- 如果先算
控制比特的关键特征
- 可以忽略不影响结果的部分
- AND:只要前面已经 0,后面的不用算
- OR:只要前面已经 1,后面的不用算
- 效率更高
- 避免无用的计算
- 在底层 CPU 指令里,这对应着“条件跳转”,可以少走一条指令
- 可能影响程序语义
- 因为短路,某些表达式里后面代码可能有副作用(比如修改变量),那部分就不执行了
- 所以写程序时要注意:布尔逻辑在 控制流 和 逻辑推理 里并不完全等价
1.4 物理比特 Physical Bit
为什么需要物理比特
- 如果一个比特要存储或传输,它必须依附在某种物理实体上
- 这个实体必须有两种可区分的稳定状态,分别代表 0 和 1
物理比特的本质
- 存储:把物体放到某个状态
- 读取:通过测量来确定状态
- 通信:如果物体在空间中移动但状态保持 → 传输信息
- 记忆:如果物体在时间上保持状态 → 存储信息
- 遗忘:如果状态被随机扰动改变 → 信息丢失
为什么关心"更小"
- 工程目标: “更小、更快、更强、更聪明、更安全、更便宜”
- 信息存储/传输的物理载体,越小越快越稳定,就越有价值
- 但这会遇到极限:当物体太小,量子效应就出现了 -> 量子比特
信息论视角
- 物理比特和抽象比特的关系:
- 抽象比特:逻辑符号,完全精确
- 物理比特:依赖物理状态,有可能受噪声影响
- 如果状态被干扰(比如热噪声、散射),比特值可能出错
- → 这就是为什么要研究 纠错编码(Error-Correcting Codes)
量子比特 Qubit
从经典到量子
- 经典比特:
- 可以复制、丢弃;
- 状态完全确定:0 或 1
- 量子比特(qubit):
- 物理载体太小,量子效应显著;
- 不能简单地用“布尔代数”来描述;
- 引入了三大关键特性:可逆性 (reversibility)、叠加 (superposition)、纠缠 (entanglement)
表示方式
- 两个基本状态不是写成数字 0、1,而是写作 ∣0⟩, ∣1⟩
- 这样做有两个好处:
- 避免和整数 0/1 混淆
- 方便推广到多个量子比特的张量积(tensor product)空间
- 这样做有两个好处:
- 物理例子:一个光子的偏振方向
- 水平偏振 = ∣0⟩
- 垂直偏振 = ∣1⟩
核心特征
(1) 可逆性 (Reversibility)
- 在量子力学中,如果某个态能演化到另一个态,那么反向过程也一定可能
- 所以量子运算本质上必须是可逆的(幺正变换)
- 但注意:
- 测量是不可逆的:一旦测量,量子态会坍缩;
- 与环境相互作用也会导致不可逆的信息丢失(退相干)
(2) 叠加 (Superposition)
- 一个 qubit 不一定只是 ∣0⟩ 或 ∣1⟩,它可以是两者的线性组合:
$∣ψ⟩=α∣0⟩+β∣1⟩$
其中$∣α∣^2+∣β∣^2=1$ - 但 测量时,只能得到两种结果之一:
- 概率 = ∣α∣2 得到 ∣0⟩
- 概率 = ∣β∣2 得到 ∣1⟩
- 测量之后,状态会“坍缩”到对应的基态
这和经典概率不同:经典概率意味着“结果已经确定,只是我们不知道”;
量子叠加意味着“结果本身就是同时存在的可能性,测量才使它确定”。
(3) 纠缠 (Entanglement)
- 两个 qubit 可以形成一个整体态,而不是独立的
- 例如:
$∣ψ⟩=\frac{1}{ \sqrt{2} }(∣00⟩+∣11⟩$ - 特点:测量一个比特会瞬间决定另一个比特的状态,即使它们相距很远
- 纠缠是量子通信和量子计算最重要的资源
不可克隆性
- Bob 如果想复制光子再测量多个方向,行不通
- 原因:复制一个未知量子态必须先测量,而测量会改变态
- 这就是著名的 量子不可克隆定理 (No-cloning theorem)
经典比特 Classic Bit
为什么需要经典比特?
- 在日常计算机中,我们并不是用单个光子、单个原子来存储信息,而是用 大量相同的物理对象(电子、电荷、光子等)
- 这时,量子效应(随机、坍缩、不可克隆)基本可以忽略,比特表现得非常稳定
- 所以我们把它建模为 经典比特:
- 可以无限次测量;
- 可以复制;
- 不会因为测量而改变状态
经典比特的测量
- 量子比特:一次测量就坍缩,不能重复测量
- 经典比特:由许多物理粒子构成,可以多次测量,几乎不受影响
- 比如:测量电压,0V–0.2V 解释为 0,0.8V–1V 解释为 1,中间区间避免使用
恢复逻辑
- 在真实电路里,电压不可能完美是 0 或 1,总会有小偏差(例如 0.98V、0.05V)
- 数字电路设计里引入了“恢复逻辑”:
- 小偏差会被电路自动纠正,恢复成理想的 0V 或 1V
- 只要噪声不超过阈值(例如 0.2V),系统就能稳定工作
- 现代计算机的可靠性就依赖于这种恢复逻辑
经典比特的特点
- 可测量,不会改变状态
- 可复制
- 对噪声有容忍度
- 是对“真实物理系统”的一种近似模型
