听 zero to hero 有些疲倦了, 想换换脑子, 受南府哥启发, 尝试一下 MIT 的这门课程

关于深度学习

什么是深度学习

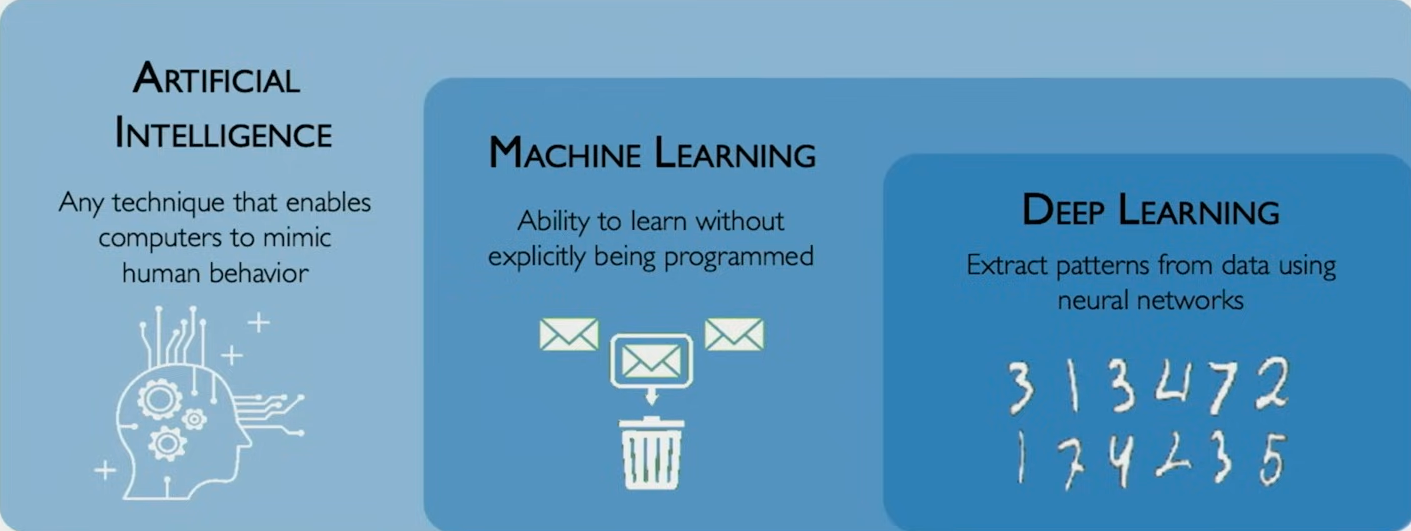
用神经网络从数据中提取特征
是机器学习的子集, 机器学习是人工智能的子集

为什么是深度学习

可以通过学习低级的特征, 进一步学习判断高级特征

为什么是现在

大数据

• 更多成熟的数据集
• 数据更易手机
• 存储设备发展

硬件

• GPU 的发展
• 并行计算的发展

软件

• 技术的提升 (各种新方法)
• 新模型
• 各种框架的发展

感知机 Perceptron

感知机是深度学习中的基本单元, 也就是"神经元"

前向传播

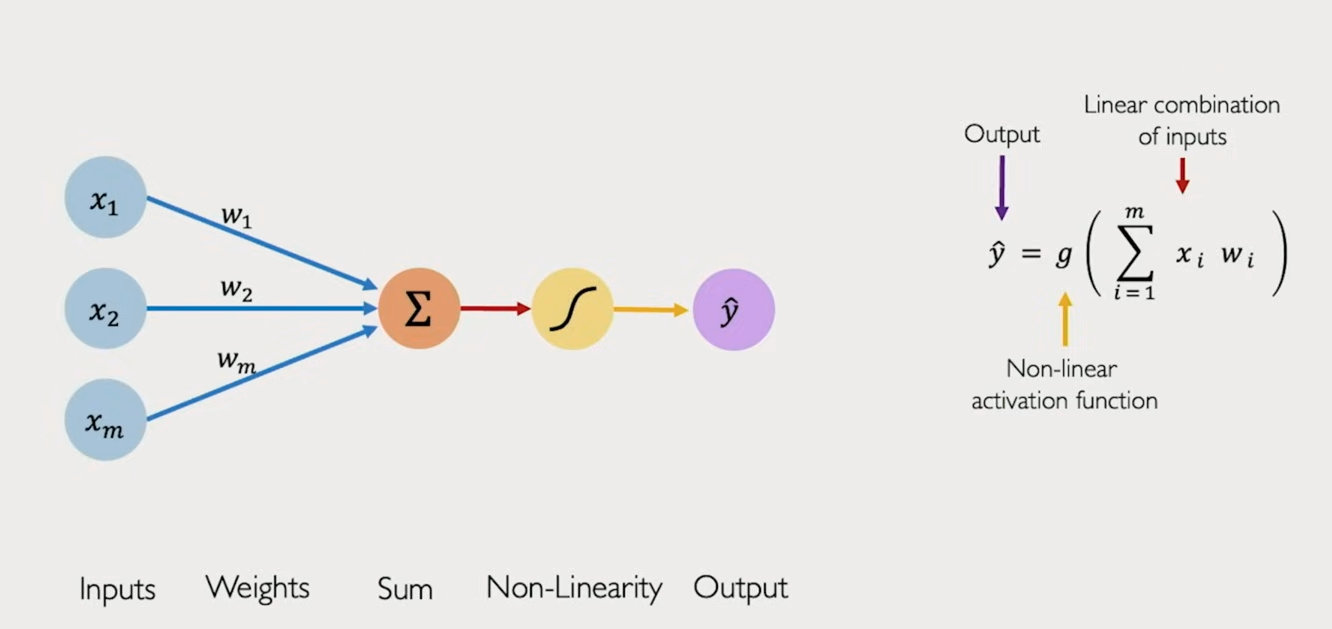
基本公式

这是每个感知机作用的基本方程: 接受输入 x, 和对应的权重 w, 经过非线性激活函数后, 得到输出 y
如果写成矩阵形式, 则是:

激活函数

为什么需要激活函数

../动手学深度学习/4.1 多层感知机
如果没有非线性函数, 那么不管模型有多少层, 归根结底都只是一个线性函数而已, 表达和拟合的能力非常有限

激活函数的种类

激活函数的种类有很多: ReLU, Tanh, Sigmoid 等等, 具体选择需要取决于使用场景

理解线性函数

这节课讲的一点让我有些启发:

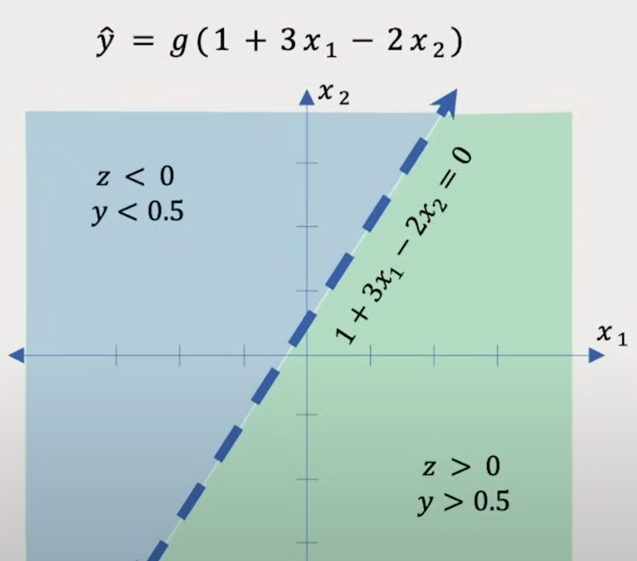
对于训练好的模型, 我们可以把 weight 和 bias 带入线性函数, 得到一个具体的函数
把函数转化为方程, 画成图像, 这里的直线相当于是一个决策边界, 把不同的输入分成了两类, 对应着进入激活函数前的值的正负
激活函数一般都是以 0 为界, 进行一些划分, 因此这个从训练好的线性函数中即可得知当前输入的情况
也就是说，神经元通过一个激活函数，将输入空间划分为不同的激活区域，进而完成对样本的分类或变换。

用感知机构建神经网络

稠密层 Dense Layer

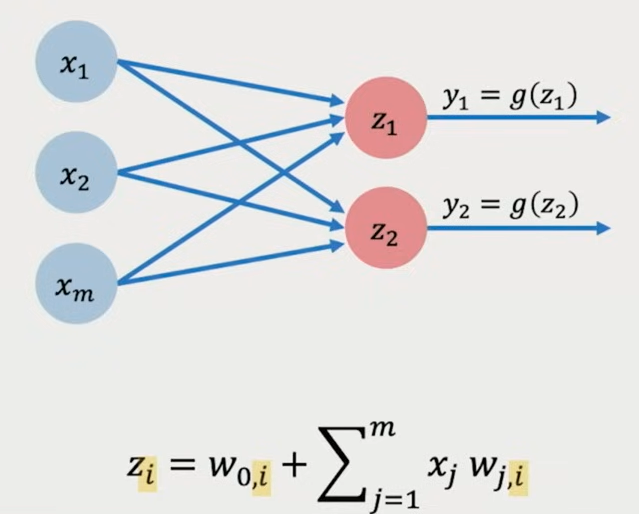
这里我们再引入一个神经元, 构成简单的神经网络
这个神经网络中, 每个神经元都接受所有的 x 作为输入 (只不过对应的 w 不同)
这种层被称为稠密层, Dense Layer

代码实现

由于我主要用 PyTorch, 所以就不写 tensorflow 的了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import torch
import torch.nn as nn

class MyDenseLyer(nn.Module):	
    def __init__(self, input_dim, output_dim):
        super(MyDenseLayer, self).__init__()
        
        # Initialize weights and bias
        self.W = nn.Parameter(torch.randn(input_dim, output_dim, requires_grad=True))
        self.b = nn.Parameter(torch.randn(1, output_dim, requires_grad=True))

    def forward(self, inputs):
    
        # Forward propagate the inputs
        z = torch.matmul(inputs, self.W) + self.b
        
        # Feed through a non-linear activation
        output = torch.sigmoid(z)
        
        return output

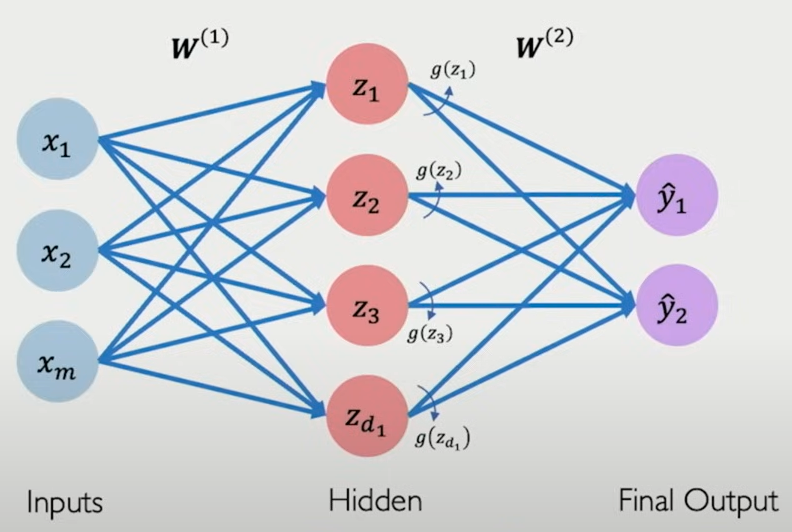
隐藏层

在刚才 Dense Layer 的基础上, 我们再引入一层网络, 这层网络被称为隐藏层 Hidden Layer, 因为无法被具体观测到, 这里的隐藏层是 z 层

1
2
3
4
5
6
7

from torch import nn

model = nn.Sequential(
	nn.Linear(m, n),
	nn.ReLU(),
	nn.Linear(n,2)
)

神经网络的应用

这里用"能否通过考试"作为一个例子, 演示如何应用神经网络解决问题

损失函数 Loss

在把相关数据输入到网络中后, 我们得到的预测值和实际值相差甚远, 这是因为模型还没经过训练. 而如何确定一个模型的好坏则需要我们思考, 因此需要引入 Loss 函数, 用于量化模型的表现

数学公式

这里的 L 是 Loss 函数, 接受经过线性变化和激活函数后得到的预测值, 与实际值进行比较. 这里是在数据集, 或者说一组数据中进行训练, 因此需除以 n 做一个平均

代码实现

Cross Entropy 交叉熵 (分类任务)

1

loss = torch.nn.functional.cross_entropy( predicted, y)

用于多分类或二分类问题，尤其适合概率输出（如 softmax 后）
适用于输出为类别概率分布，predicted 是网络输出（未 softmax），y 是标签索引（不是 one-hot 编码）。

MSELoss 平均损失 (回归任务)

1

loss = torch.nn.functional.mse_loss(predicted, y)

用于连续值预测（例如预测分数、价格等）：
适用于数值型回归问题，predicted 和 y 都为实数张量。

训练神经网络

优化 Optimization

我们希望找到一个合适的 weights, 使得 loss 最小

梯度下降

可以想象一下 loss function 和 w 组成的超平面:

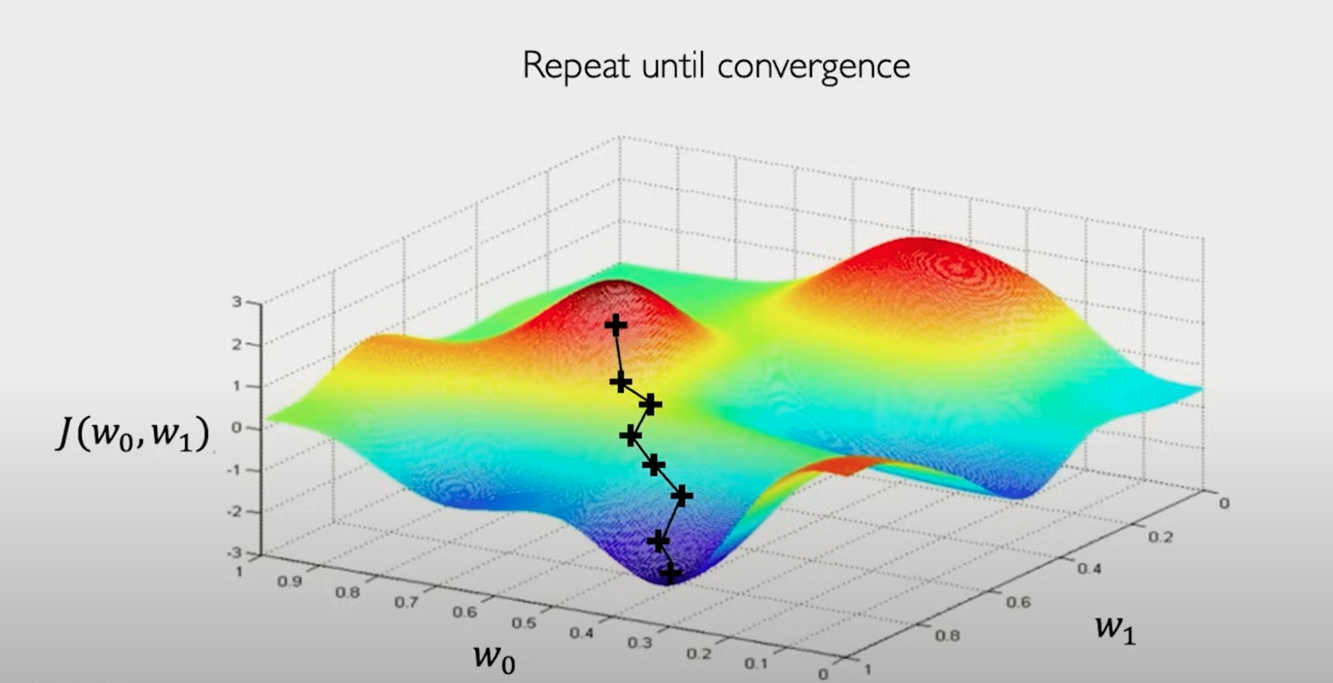
首先我们随机选取一个点, 然后计算当前点的梯度, 也就是上升速度最快的方向, 沿着反方向更新 w, 直到到达 local minima 局部最小值

伪代码

1. 随机初始化权重
   $$ \mathbf{W} \sim \mathcal{N}(0, \sigma^2) $$
2. 循环, 直至收敛或停止
3. 计算梯度

4. 更新参数 $$
   \mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial J(\mathbf{W})}{\partial \mathbf{W}}

   $$

   $$

5. 返回最终权重

反向传播

写过太多次了, 懒得再写了
../动手学深度学习/4.7 前向传播、反向传播和计算图

优化

这里单独把 optimization 拿出来说一说, 涉及到一些技巧

设置学习率

在 error surface 上更新参数时, 很容易卡到局部最小值上, 因此需要通过合理设置每次迭代的"步长", 尝试跨过局部最小, 使得走到更低的 loss

解决方法

1. 不断手动调试, 找到相对表现更佳的学习率的值
2. 设置自适应学习率算法

自适应学习率

自适应学习率需要考虑众多因素作为该算法的"参数", 比如:

• 梯度
• 权重
• 先前的 lr

常见自适应算法

• SGD
• Adam
• Adadelta
• Adagrad
• RMSProp

后面懒得写具体内容了, 基本之前都学过

小批量 mini-batch

过拟合

避免过拟合 : 正则化 Regularization

Dropout

早停 Early Stopping