Word Vectors

继续讲讲词向量

为何区分context和center?

其实在lec1 的时候我就萌生了这个疑惑, 并且得到了 gpt 的解答
【CS224N】Lec 1 - Intro and Word Vectors
lec2 中有同学提出了同样的问题, 教授的解答给了我另一个角度:

当确定一个中心词, 遍历上下文时, 当遇到和他相同的词, 如果不对 center 和 context 向量加以区分, 会出现二次项, 甚至高次项的情况, 会比较难处理

不过对于最终的 word 对应的 vec, 大概就是 context 和 center 取的平均值

统计词语间共现次数

想法

在训练词向量的时候, 我们需要反复遍历整个语料库, 为何不直接统计共同出现过的词? 以反应词语间的关系

具体做法

建立共现矩阵 X, 行和列是单词, 对应坐标的值是共现次数

窗口共现

在每个词的窗口统计上下文, 可以捕捉到一定的句法和语法信息, 反映词空间结构

全文档共现

统计词在文档中出现次数, 适合抓取文章主题, 得到向量更加偏向"主题空间"

矩阵降维

使用共现次数这个方法会导致共现矩阵维数很高，很难处理。
这里需要用到线性代数的知识，借助 奇异值分解（SVD） 的方法进行矩阵降维。

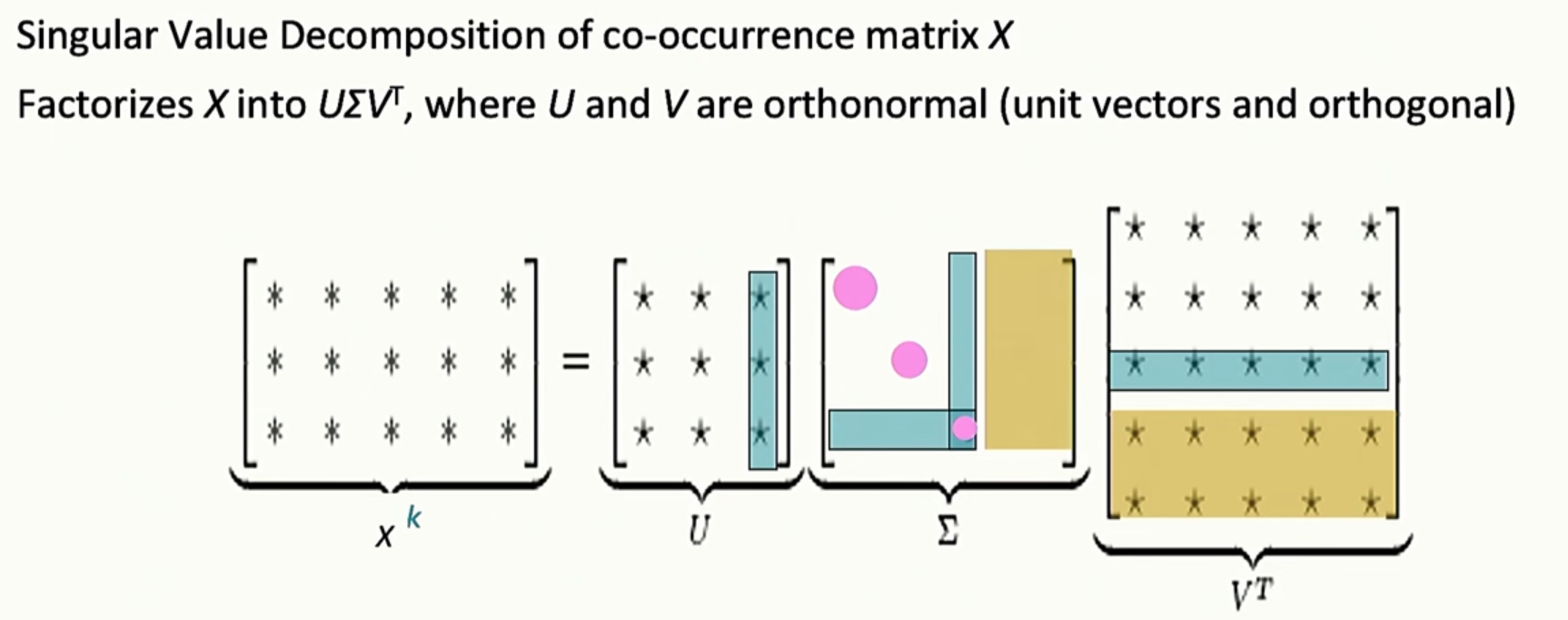
../../source/矩阵降维.png
这里我们对中间的 Σ 矩阵中的奇异值（主对角线上的数）从大到小排序，只保留最大的前 $k$ 个奇异值及其对应的 $U$、$V^T$ 的列/行（即主成分）。
这样就能用更低的维度近似还原原始矩阵 $X$，既减小了存储和计算复杂度，又保留了最核心的信息。
这些主成分通常代表了词对之间最强的关联或主要的语义结构。

补充说明：

$\Sigma$ 矩阵中的每一个较大的奇异值，分别对应 $U$ 和 $V^T$ 矩阵中一组主方向（即一列和一行）。
只保留最大的 $k$ 个奇异值和对应的方向，就实现了有效的降维。
这样不仅可以压缩数据规模，还能提取出数据中最重要的结构信息，常用于文本挖掘、推荐系统、图像压缩等场景。

COALS

这也是一种降维的方法, 同样借助 SVD, 不过在上面的基础上做了一些改进

原有缺点

直接在原始词频上做统计, 导致一些无意义的词(he, she, the)成为出险次数最多的
模型并没有学到语义信息, 而是语法规律

改进方法

对词频取对数 log: 可以有效抑制高词频的影响
设置词频上限: 避免被过高的词频干扰
忽略功能词
加权窗口: 根据窗口远近设置权重, 体现语义相关性
使用皮尔逊相关系数代替贡献数: 更好地捕捉词语间的相关性

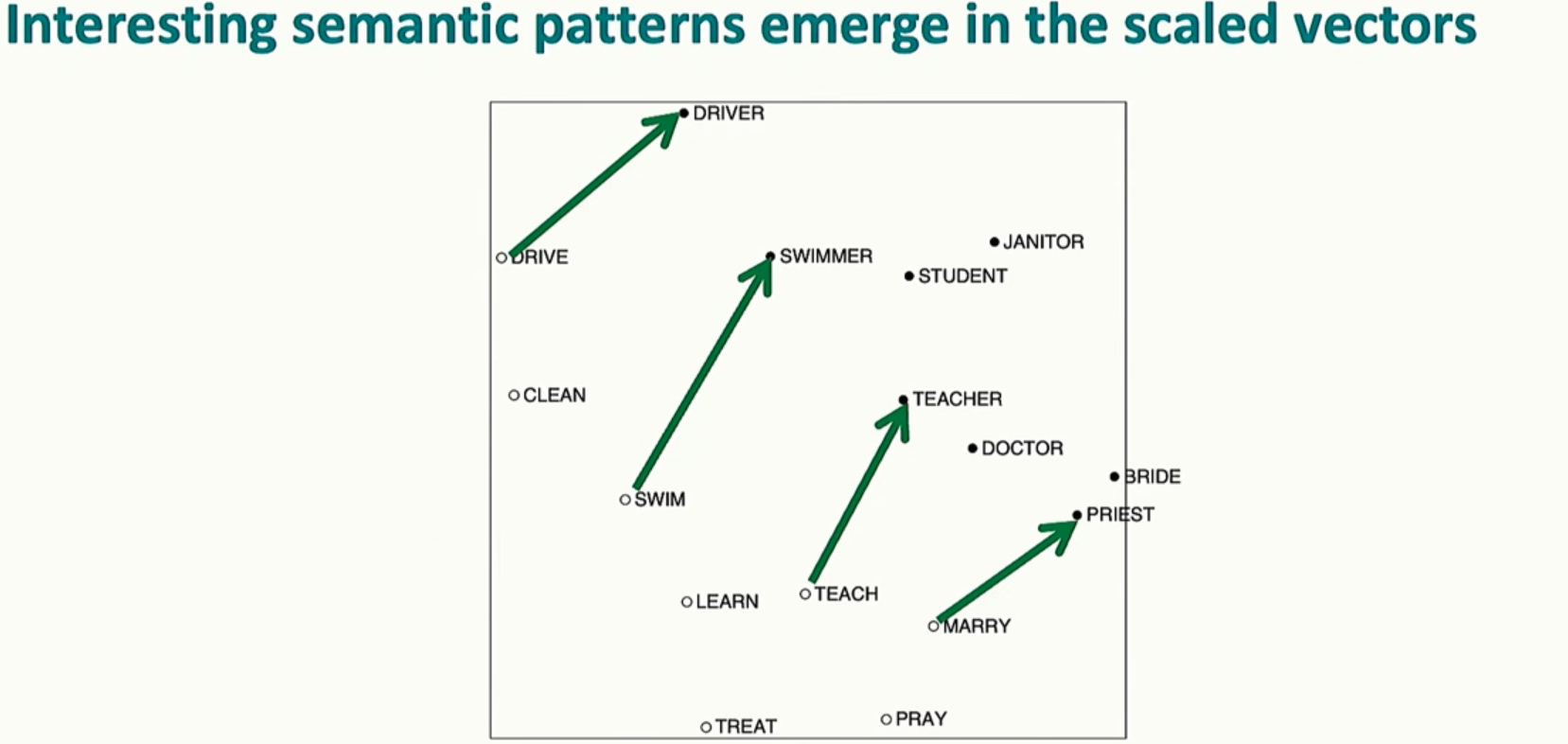
意外发现

经过一些技巧性地处理, 然后再降维后, 我们发现 COALS 模型同样具有语义方向, 和之前讲的 word2vec 有相似的属性
../../source/线性语义.png

GloVe

捕获语义

刚才 COALS 的结果让我们了解到共现次数可以在处理后表示一定的语义, 我们想要通过一些方式来捕获它
通过计算共现概率, 我们可以获取到目标词汇的一些性质
../../source/捕获线性语义.png
通过计算这些比率, 我们可以了解到 x 相关的语义信息, 其中比率大小表示 x 与对应词语的相关程度

用向量差反映语义关系

对数双线型模型

$$ w_i ⋅ w_{j} =\log{P(i\mid j)} $$

可以用词向量的内积表示对应条件概率的对数

向量差表示比率

利用对数的性质, 我们可以用向量差来表示比率

$$ w_{x}⋅(w_{a}-w_{b}) = \log \frac{P(x|a)}{P(x|b)} $$

损失函数

$$ J = \sum_{i,j=1}^{V} f(X_{ij}) \left( \mathbf{w}_i^\top \tilde{\mathbf{w}}_j + b_i + \tilde{b}_j - \log X_{ij} \right)^2 $$

$X_{ij}$：词 $i$ 和词 $j$ 的共现次数。
$\mathbf{w}_i$ 和 $\tilde{\mathbf{w}}_j$：词的两个向量表示，分别对应目标词（word）和上下文词（context）。
$b_i$ 和 $\tilde{b}_j$：对应的偏置项。
$f(X_{ij})$：权重函数，常见选择是
$$ f(x) = \left( \frac{x}{x_{\max}} \right)^\alpha $$
用于降低高频词对损失的影响。

GloVe 通过最小化上述损失，让词向量能够捕捉共现概率的对数关系，从而在向量空间中表现出语义的线性结构。

我的理解是, 这里需要把压缩维度后的 w 矩阵和 b 继续训练, 让他们能够正确地通过对数双线性模型表示语义信息.

评估模型

一词多义

向量叠加

对于一词多义的情况, 我们实际上会对每个意思都学到一个对应的向量, 而最终该词对应的向量是各个含义向量的加权平均, 其权重是出现频率

重建语义向量

对于已知最终向量的情况, 可以利用稀疏编码理论, 在高维且稀疏的空间中重构语义向量

构建神经网络分离器

分类问题

我们这里使用监督学习, 需要有训练数据集
其中, 训练数据集由许多对(x,y)组成
其中, x 是输入数据; y 是对应的标签, 在这里应该是 x 对应的类别
训练数据用来训练模型

分离器

../../source/分离器.png

softmax分离器

softmax 分离器通过构建线性函数, 并更新矩阵参数, 使得预测正确率最大化
然而这里的分类空间是线性的, 不够灵活

神经网络分离器

神经网络分离器不仅学习权重矩阵 W 的参数，还能同时学习输入（如词语）的分布式表示（词向量）
词向量不再是简单的 one-hot 独热编码，而是能表达语义信息的低维稠密向量，通过嵌入层学习得到
此外，神经网络通过多层非线性变换，可以将原本线性不可分的数据映射到可以线性分的空间，从而实现更复杂、更灵活的决策边界，大幅提升分类器的表达能力和准确率

交叉熵

$$ H(p,q)=-\sum^C_{c=1} p(c)\log q(c) $$

这其实涉及一些信息论的知识, 后面会补一补的
大概就是, 对于两个分布 p 和 q, 若越接近, 则交叉熵损失越低, 表明模型效果越好
这里的 p 是 label, 在分类问题中的分布应该对应的是一个 onehot
所以交叉熵函数就变成了, 对应 label 在预测的分布中, 概率的 -log 值