神经网络的发展

第一次爆发

第一次快速发展是在 21 世纪初, 主要有 Hinton 等元老推动
但是当时面临的一个很现实的问题是: 只能训练较浅的网络
这导致神经网络并没有很好的实际应用效果, 缓慢发展

解决方法

正则项

在损失函数中添加正则项可以优化神经网络的训练
这里的正则项又称为"惩罚项", 可以避免模型学得太复杂而导致过拟合的问题

$$ J(\theta) = \frac{1}{N} \sum_{i=1}^{N} -\log \left( \frac{e^{f_{y_i}}}{\sum_{c=1}^C e^{f_c}} \right) + \lambda \sum_k \theta_k^2 $$

L2 正则项

这里公式末尾加上的就是 L2 正则项
具体来说, 是把模型中每个参数求和, 然后乘以一个系数, 防止参数太大

我的疑问: 参数太大代表模型复杂?

我认为:参数太大跟模型复杂没有直接关系?

详细询问 GPT 后, 得到了答案:
参数太大, 意味着对应的神经元会对输入变化很敏感. 同时, 模型的函数曲线也会变得很陡峭, 极端
加入 L2 正则项后, 可以避免模型被计算噪声干扰, 使得函数更加平滑, 有比较好的泛化能力

Dropout

这种方法是在训练中, 随机地将网络中的一些神经元的输入设置为 0, 进行训练.
这个和随机丢弃一部分神经元等效, 是为了避免神经元之间相互依赖, 或者对于某个神经元过度依赖
通过随机 Dropout, 可以有效提升模型的灵活度, 使得它能学到更好地灵活利用不同神经元代表的不同特征进行判断

理论解释

Manning 把 Dropout 这种方法比作介于两类模型之间:

Naive Bayes：每个特征的权重独立（互不影响）
Logistic Regression：所有特征权重一起学（彼此影响）

Dropout 让模型既能独立思考（像 Naive Bayes），又能学会组合（像 Logistic 回归），取得平衡。

向量化

这里的向量化是指, 将原先依赖与 for 循环的向量运算, 合并为矩阵运算
这样能大大提升计算效率, 缩短计算时间

参数初始化

随机初始化

必须采用随机初始化权重, 不能全为 0
全为0 会导致所有神经元都一样, 网络具有对称性, 无法学习到多样化特征
较小的随机值可以使得网络高效学习
../NN Zero to Hero/【NN Zero to Hero】Makemore - part 3
zero2hero 中也提到过这个问题, 不过是另外一种视角: 零矩阵会导致计算图中相关部分的丢失

优化器 Optimizer

SGD

基本情况下, SGD 可以胜任大部分工作. 然而, 它比较依赖人工调参, 通过手动调整步长等超参数寻找最优情况

还有不少更好, 更现代化的优化器, 可参考图中
$../../source/Lec 5 - Recurrent Neural Networks\_optimizer.png$

语言建模

定义

语言建模是指预测下一个词的任务
详细来说 : 对于给定的单词序列, 计算下一个词的概率分布

n-gram 语言模型

其中 n 表示基于前 n 个单词, 以预测下一个单词的概率分布

马尔科夫假设

首先, 做出马尔科夫假设:
下一个词的出现情况只依赖前 n 个词

稀疏性问题

概率中的某个单词可能从未出现过, 因此会导致概率为 0, 无法继续计算的情况

引入微小量

主要针对分子为零–概率为零的情况
主要的解决方法是加入一个微小量 $\delta$ , 使得概率不为 0, 且不会影响大致的概率分布

backoff 回退

主要针对分母为零–无法计算概率的情况
由于 n-gram 从未出现, 因此退而求其次统计(n-1) - gram 的次数, 以此类推

矛盾

为了得到更好的预测结果, 需要尽可能增大 n
增大 n 会带来更大的存储和计算压力, 以及更严重的稀疏性问题

神经网络模型

基本结构

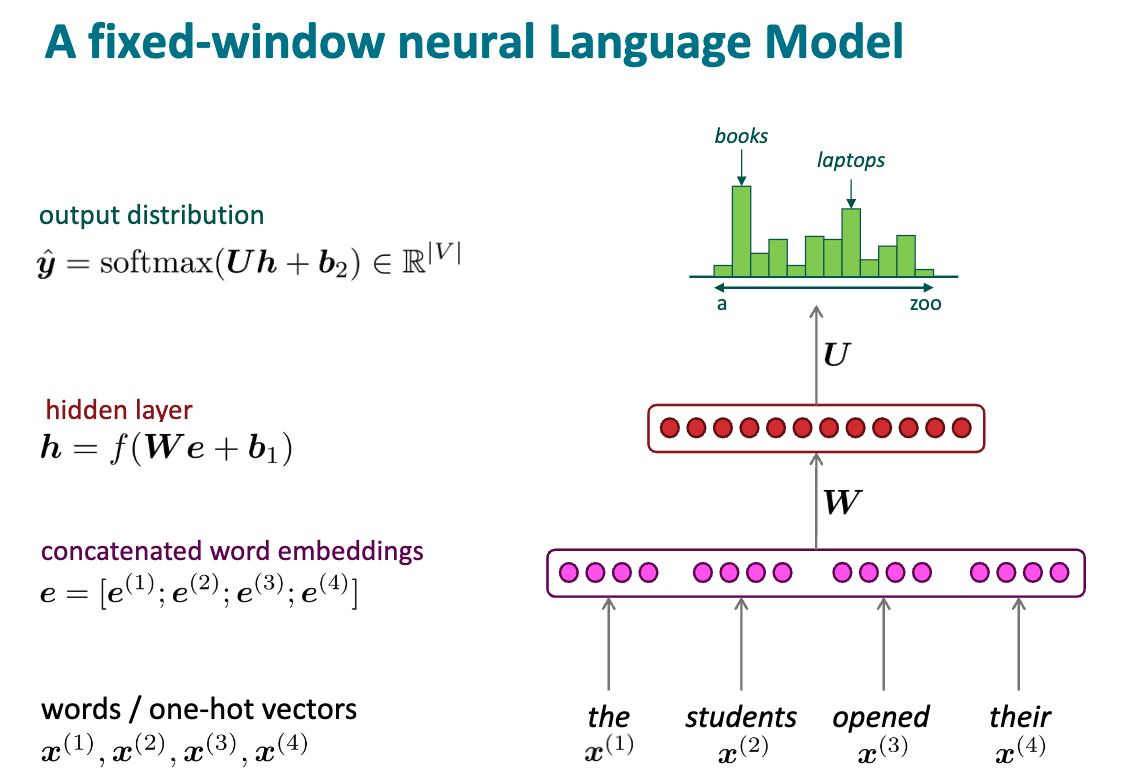
$../../source/Lec 5 - Recurrent Neural Networks\_神经语言模型.png$

把每个词转换成对应的独热向量, 或者词向量
将各个词按照窗口大小拼接起来, 拼成一个向量
隐藏层, 其中包括线性层和非线性激活函数
用 softmax 将 logits 转换为概率分布
对概率分布进行采样, 得到预测的下一个词

提升与不足

提升

不再有稀疏性问题
不需要存储所有观测到的 n-gram 组合

不足

固定的窗口太小–上下文太短
增大 window 需要增大矩阵 W
每个词语的地位相同, 无法注意到更重要的部分

循环神经网络 RNN

基本结构

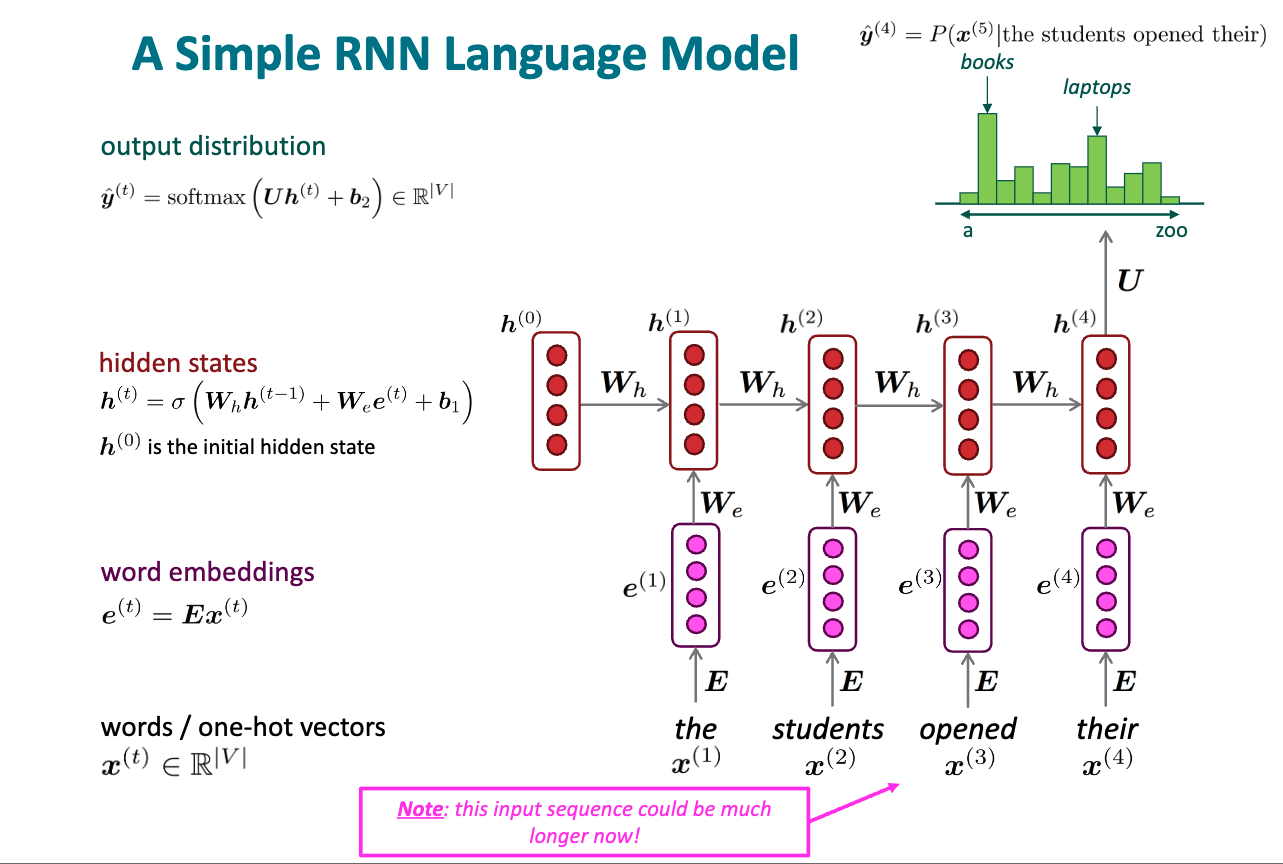
$../../source/Lec 5 - Recurrent Neural Networks\_RNN.png$

将词语转换成嵌入向量/词向量
用新的词语更新隐状态 hidden state
对更新后的隐状态进行计算, 得到概率分布, 进行采样, 得到预测的下一个词

优点与不足

优点

能处理任何长度的输入: 一个一个读入
当前的计算可以使用很多个时间步之前的信息:隐状态包含历史信息
对于更长的输入上下文, 模型大小不会增加:只和模型设计大小有关
每个时间步使用的权重相同, 存在某种对称性

缺点

计算速度太慢
难以访问很久远的历史信息:理论上可以, 但是容易梯度消失/爆炸

训练 RNN

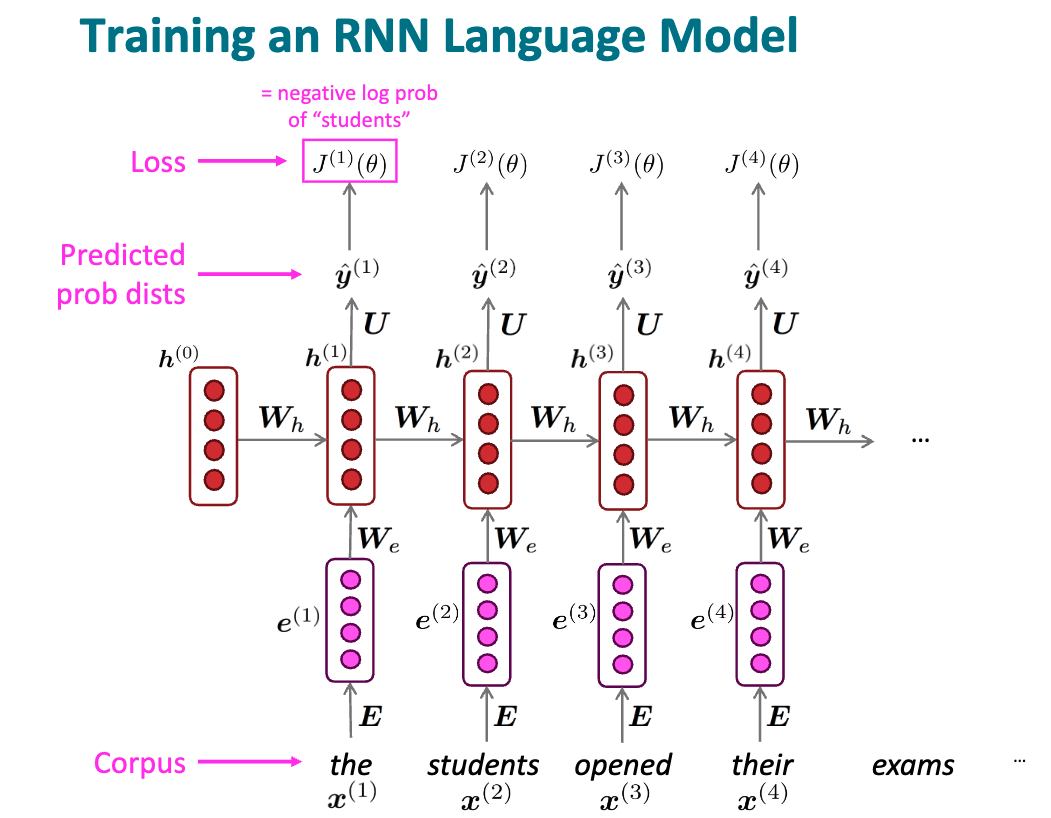
$../../source/Lec 5 - Recurrent Neural Networks\_training rnn.png$

找到一个大的语料库
把词输入到 RNN 中, 计算每个时间步输出的概率分布
计算单步损失 loss

$$ J^{(t)}(\theta) = CE(\mathbf{y}^{(t)}, \hat{\mathbf{y}}^{(t)}) = -\sum_{w \in V} y^{(t)}_w \log \hat{y}^{(t)}_w = -\log \hat{y}^{(t)}_{x_{t+1}} $$

对每一步的算是加和求平均

$$ J(\theta) = \frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta) = \frac{1}{T} \sum_{t=1}^{T} -\log \hat{y}^{(t)}_{x_{t+1}} $$

基于 loss, 更新网络中的参数 : 直接基于整个预料库更新的计算量巨大, 可以借助 SGD, 进行小批量更新

用 RNN 生成文本

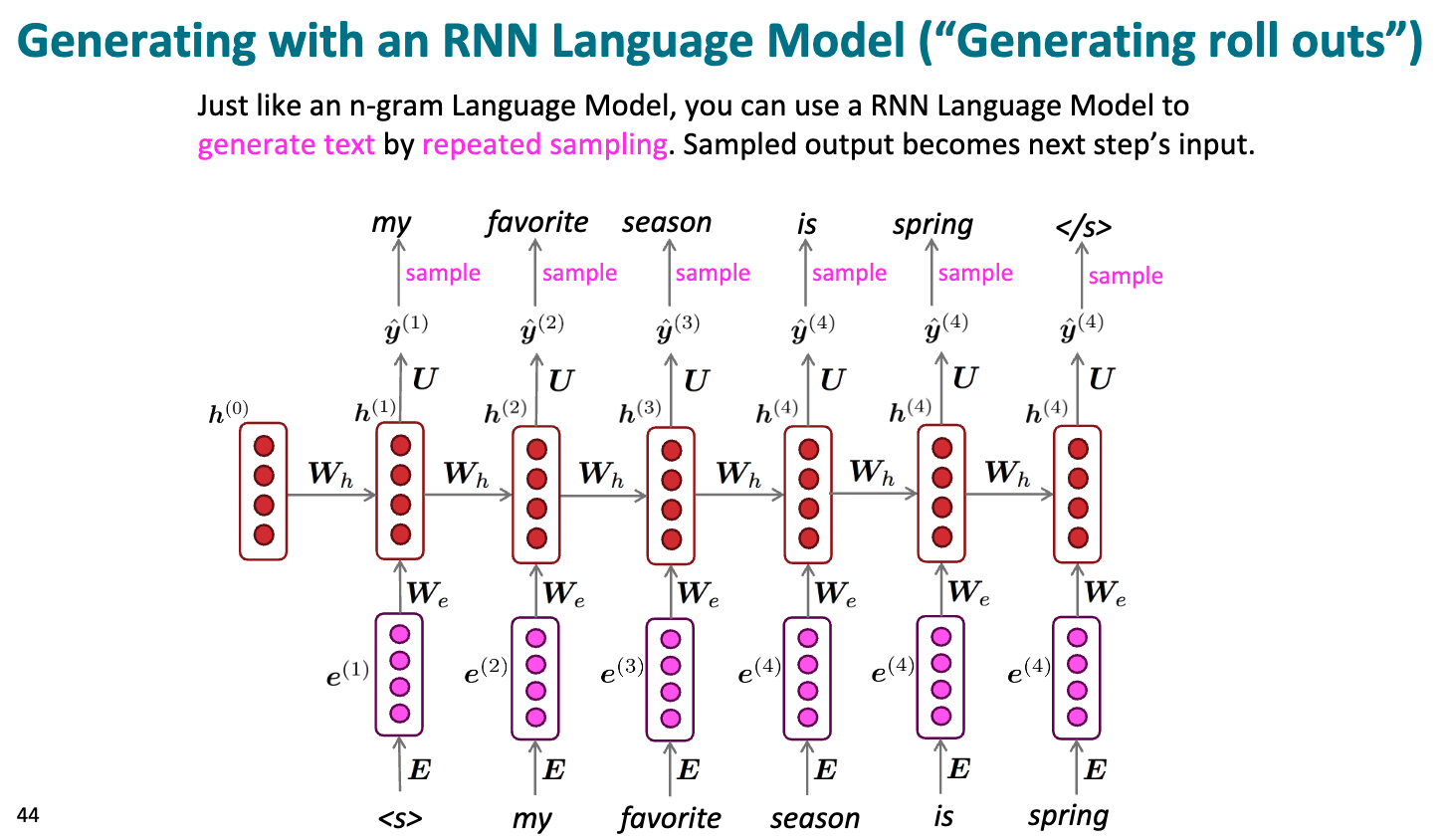
$../../source/Lec 5 - Recurrent Neural Networks\_生成文本.png$

把输入传到 RNN 中, 经过计算采样得到第一个输出, 然后把输出作为预测的单词, 再传到 RNN 中, 以预测下一个单词, 循环往复
在某些条件下, 输出终止符, 表示生成完毕.