评估语言模型

评估方法

收集真实语句
给定前面的词, 用模型预测下一个词的概率分布
对于真实情况中的下一个词, 查找并记录对应的概率
汇总所有概率, 计算评估指标

评估指标

困惑度 Perplexity

Perplexity（困惑度）：语言模型最常用的评估指标，反映模型“有多困惑”，值越低越好

$$ \text{perplexity} = \left( \prod_{t=1}^T \frac{1}{P_{\text{LM}}(x^{(t+1)} \mid x^{(t)}, \ldots, x^{(1)})} \right)^{1/T} $$

其中 $P_{LM}(x(t+1)∣x(t),…,x(1))$ 表示语言模型在给定前面所有词时预测下一个词的概率。
这个乘积是所有词的逆概率，开 T 次方是为了归一化（相当于“按单词数归一”）

交叉熵

$$ J(\theta)= \left( \prod_{t=1}^T \frac{1}{\hat{y}_{x_{t+1}}^{(t)}} \right)^{1/T} = \exp \left( \frac{1}{T} \sum_{t=1}^T -\log \hat{y}_{x_{t+1}}^{(t)} \right) = \exp(J(\theta)) $$

上面困惑度的公式其实是与交叉熵损失的指数形式等价的

RNN 的梯度消失与爆炸

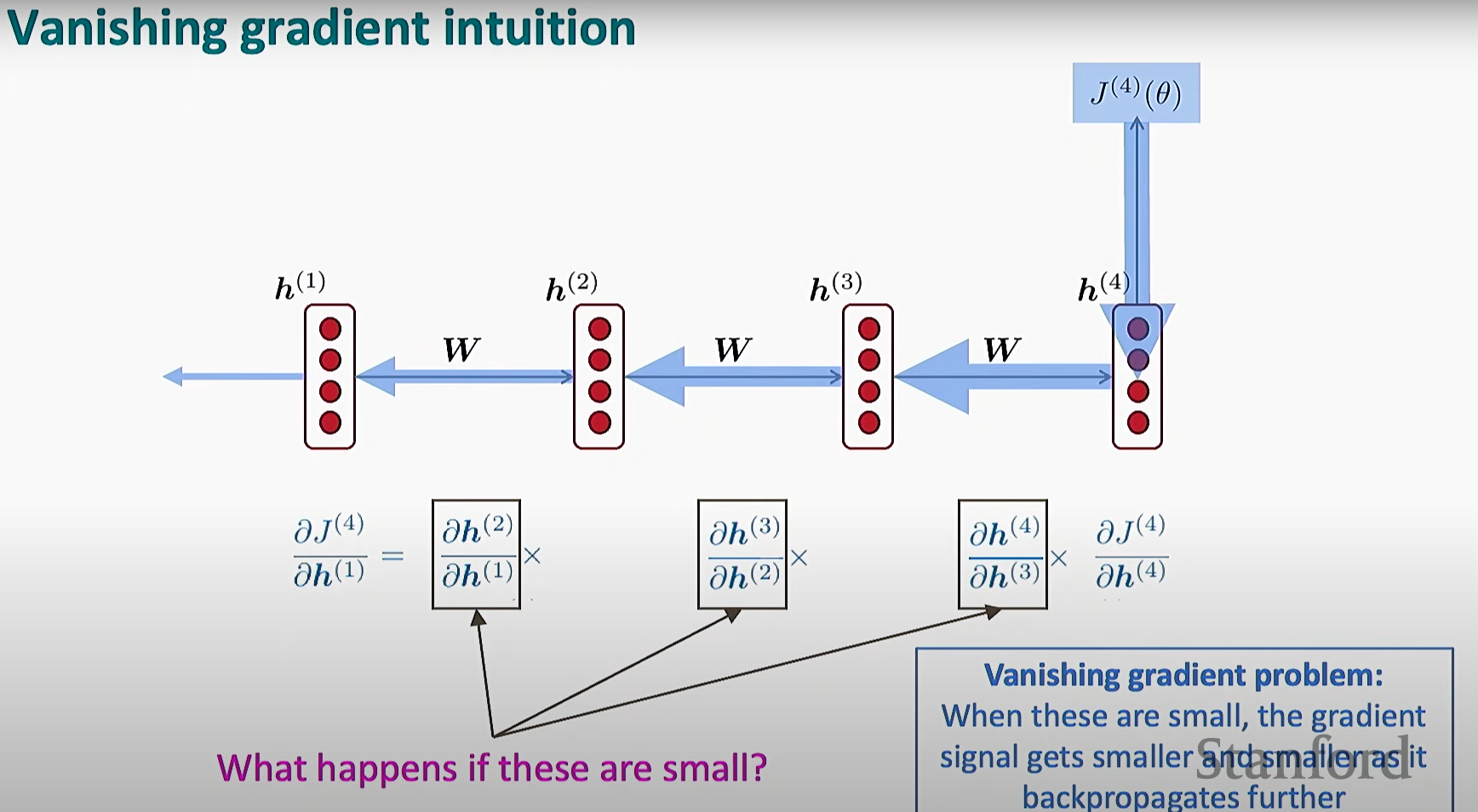
$../../source/Lec 6 - Sequence to Sequence Models\_梯度消失与爆炸.png$
根据损失函数, 进行反向传播并更新参数, 其间需要处理多个时间步的偏导数相乘的问题, 随着时间步的增加, 梯度面临着**梯度消失(极小, 趋于零) ** 或者 梯度爆炸(极大, 趋于无限/溢出) 的问题

梯度消失

由于梯度趋于零, 导致神经网络无法基于梯度更新参数
因而不能很好的更新隐状态, 失去了对于远时间步信息的"记忆"
通过使用激活函数等方法, 可以缓解这一问题, 但无法彻底解决.
因此需要考虑其他架构, 使得拥有更好的记忆能力

梯度爆炸

由于梯度溢出, 导致神经网络每次更新的"步子迈得过大", 使得训练效果不理想, 且不稳定

解决方法:梯度裁剪

这个方法简单粗暴:

为梯度设定一个阈值, 作为上限
如果梯度范数大于预设的阈值），就缩放梯度，使它的大小等于阈值，但方向不变。

1
2
3
4


g_hat ← ∂E/∂θ
if ||g_hat|| ≥ threshold then
    g_hat ← threshold / ||g_hat|| * g_hat
end if

LSTMs 长短期记忆网络

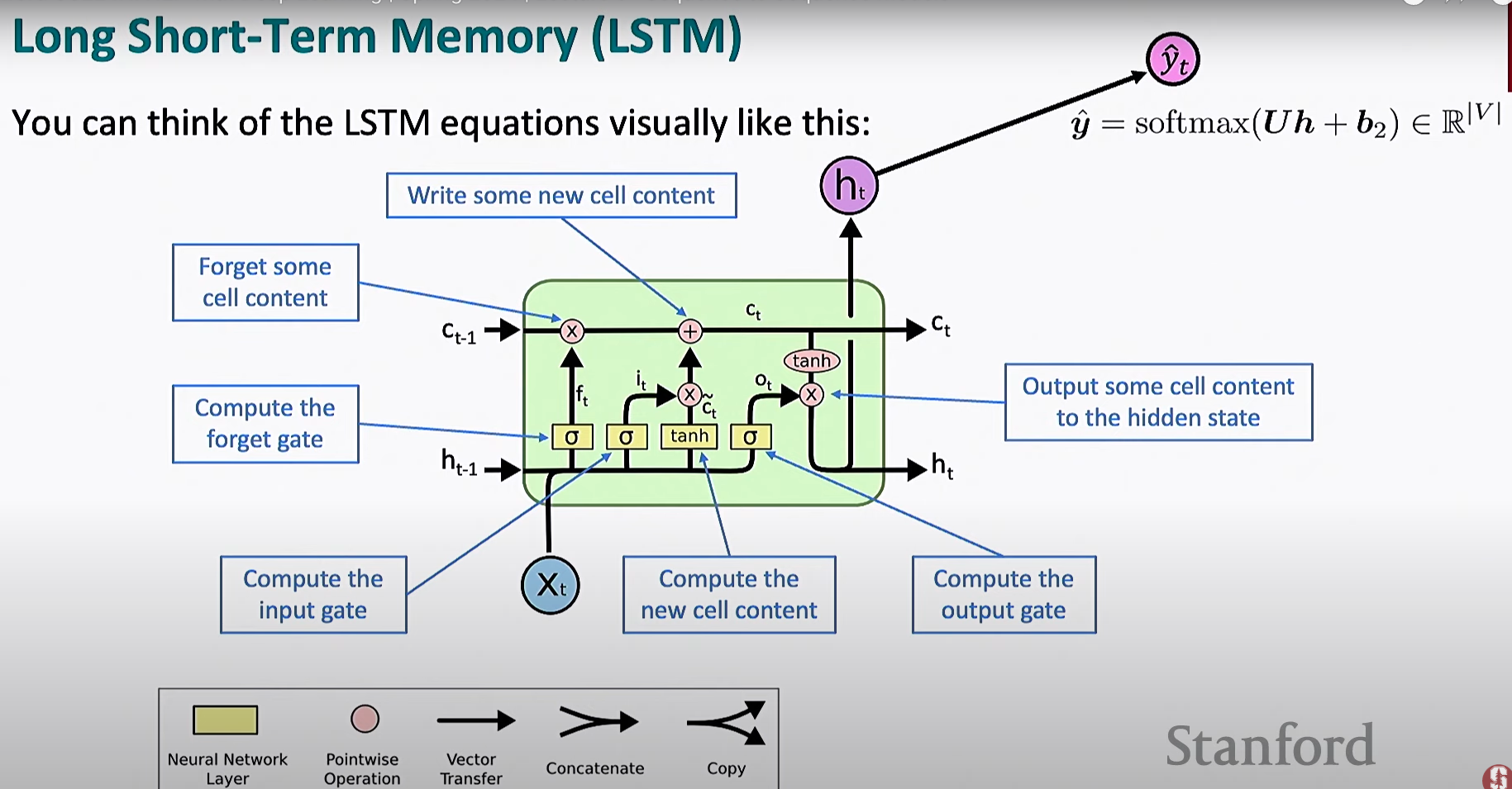
$../../source/CS224NLec 6 - Sequence to Sequence Models\_lstm-1.png$

门控机制

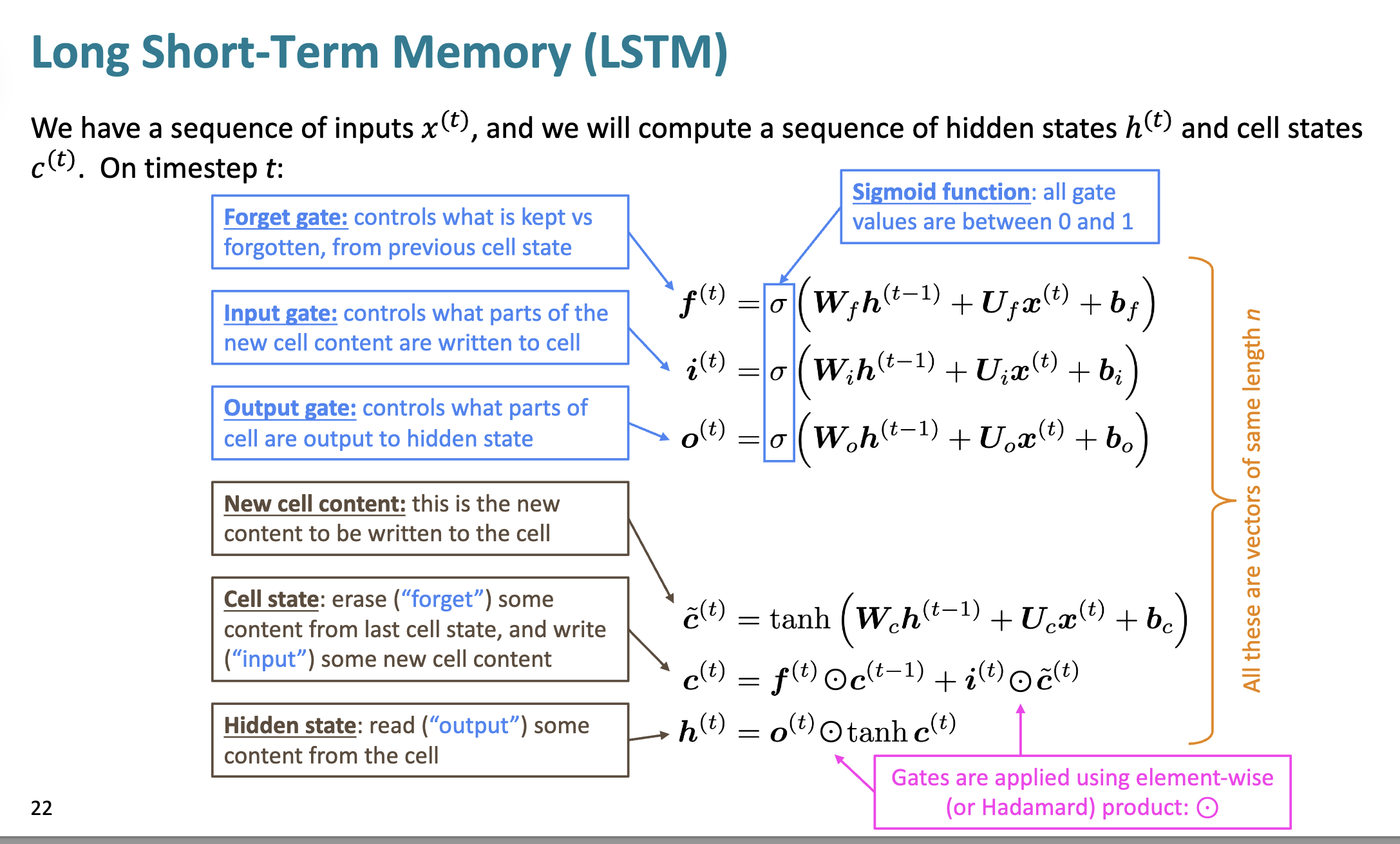
$../../source/Lec 6 - Sequence to Sequence Models\_LSTM.png$
LSTM 网络中引入了门控机制, 用于控制信息的流动和保留

遗忘门

这里虽然叫遗忘门, 但其实是"记忆门", 用来控制记忆/遗忘多少单元状态的东西
$f^{(t)} = \sigma ( W_f h^{(t-1)} + U_f x^{(t)} + b_f )$
接受前一个隐状态, 通过 U_f 对当前输入进行评估, 综合计算求和, 经过 Sigmoid, 得到在区间 0 - 1内的数值
越接近 0，越遗忘；越接近 1，越保留

输入门

决定新的输入要向细胞中写入多少东西
$i^{(t)} = \sigma ( W_i h^{(t-1)} + U_i x^{(t)} + b_i )$
运算方法差不多
越接近 0, 新内容写入越少; 越接近 1, 新内容写入越多.

输出门

决定当前细胞内容有多少要被输出到隐状态中
$o^{(t)} = \sigma ( W_o h^{(t-1)} + U_o x^{(t)} + b_o )$
越接近 0, 代表输出门关闭, 当前状态内容输出到隐状态中越少;
越接近 1, 代表输出门打开, 当前状态内容输出到隐状态中越多.

记忆细胞

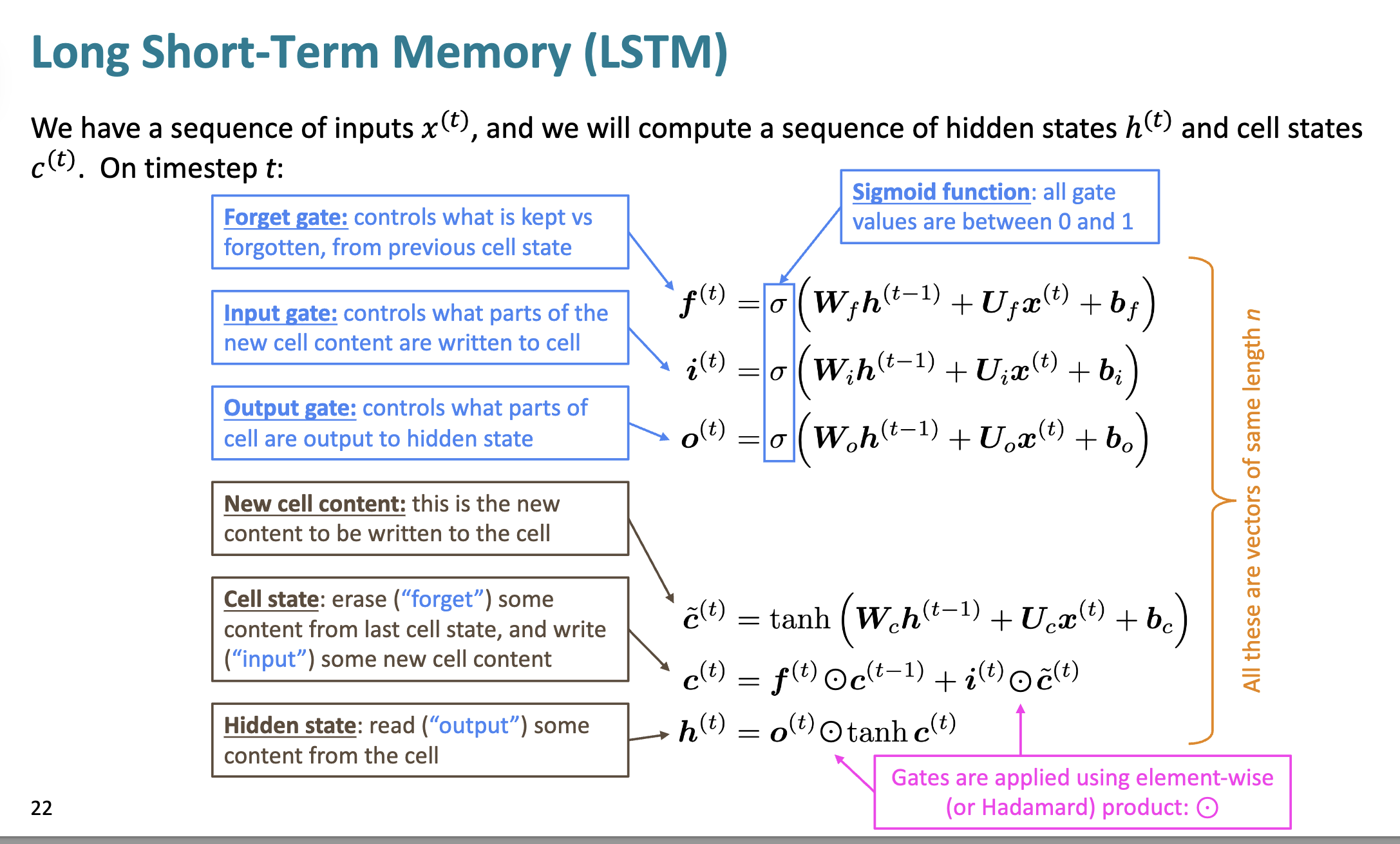
../../source/Lec 6 - Sequence to Sequence Models.png
在 RNN 已经有了"隐状态"这个部分, 而 LSTM 再此基础上引入了单元状态 Cell state 这个概念

隐状态

隐状态在这里作为当前的输出快照, 是短时记忆
主要表示当前的特征表达
用于作为下一个时间步的输入，也常常被拿去做下游任务
每个时间步都会对外输出（比如用作下一个 LSTM 单元、或者作为模型最终输出）

计算

$h^{(t)} = o^{(t)} \odot \tanh \left( c^{(t)} \right)$

单元状态

单元状态是长期记忆, 主记忆
作为记忆的高速信息通道, 可以在很多时间步之间无损地传递信息
能够记住很远的信息，解决梯度消失
通常不直接作为模型输出，而是为内部长期记忆服务。

计算

$ c^{(t)} = f^{(t)} \odot c^{(t-1)} + i^{(t)} \odot \tilde{c}^{(t)}$

设计动机 : 我的理解

猜测的思路

lstm 主要是为了实现长期记忆, 引入了单元状态. 为了区别于隐状态, 并且实现计算和更新, 所以需要引入门控机制来控制信息的流动与存储

为什么需要引入单元状态?

易被污染的隐状态

在 RNN 中, 隐状态既要参与输出, 也要参与输入, 存储的信息容易被污染/稀释

梯度问题

RNN 中, 在反向传递过程中, 由于链式法则带来的一长串相乘, 容易引发梯度消失/爆炸

信息丢失

在接受输入实现更新后, 隐状态的信息很难被恢复

单元状态的梯度问题?

这里我又产生另一个疑问: 引入单元状态后, 单元状态不会面临相似的梯度问题吗?

对于单元状态, 其沿着主线传递, 大部分是线性加权累加

$$ c^{(t)} = f^{(t)} \odot c^{(t-1)} + i^{(t)} \odot \tilde{c}^{(t)} $$

因此:

梯度可以几乎无损的在单元状态间传递
只要门控参数训练得当, LSTM 可以记忆很久, 让梯度流得很远

【CS224N】Lec 6 - Sequence to Sequence Models