内存统计 Memory accounting

张量基础 tensors basics

• 张量是深度学习中存储一切信息的基础构建

张量内存 tensors memory

• 几乎所有重要张量都以浮点形式储存
  • 参数, 梯度, 激活值…..

float32

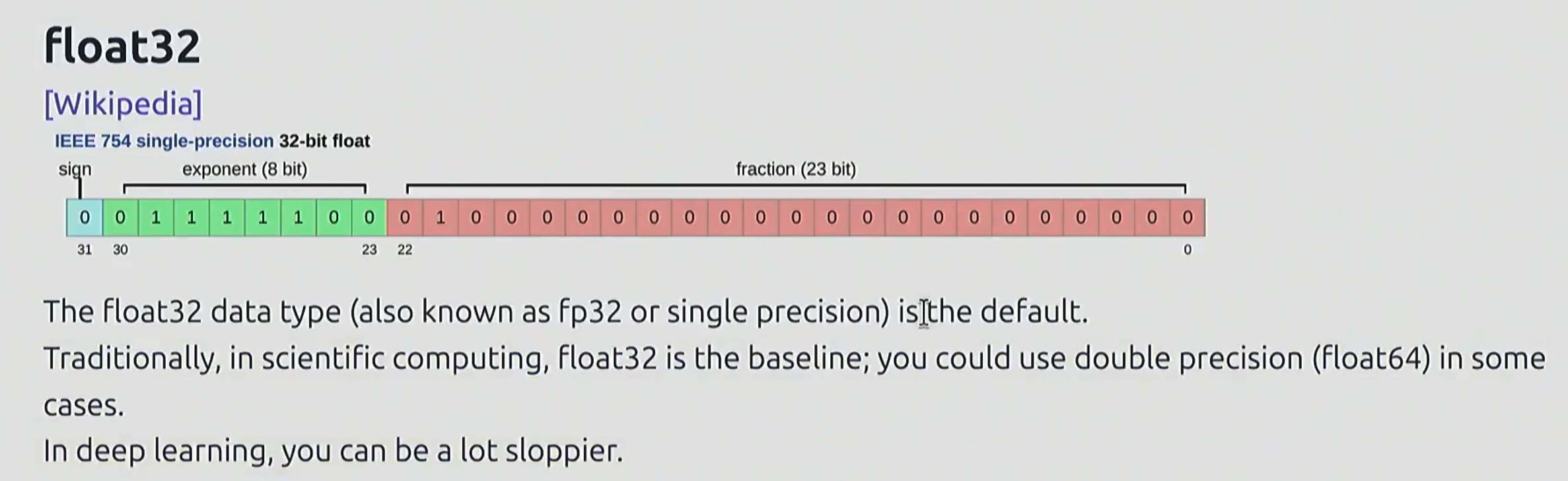
一共占 32 bits, 其中 1 位表示符号, 8 位表示指数, 23 位表示小数

基本信息

• 又叫做 fp32, 单精度. 是默认数据类型
• 在深度学习领域, 由于在数据精度上不拘小节, fp32 已经是上限了

内存占用

float16

• 16bits, 其中 1 位符号, 5 位指数, 10 位小数
• 被称为 fp16, 半精度
• 动态范围不太理想, 因此在训练中可能不太稳定

bfloat16

• Google Brain 提出, 称为 brain floating point
• 专门用于解决动态范围小的问题
• 这里增加了用于表示指数的 bits, 减少了用于表示小数/分数的 bits, 使得用 16 bits 即可达到 float32 的动态范围
• 对于深度学习, 小数的精度相比于指数数量级 没有那么重要
• 通常用 bf16 进行运算

fp8

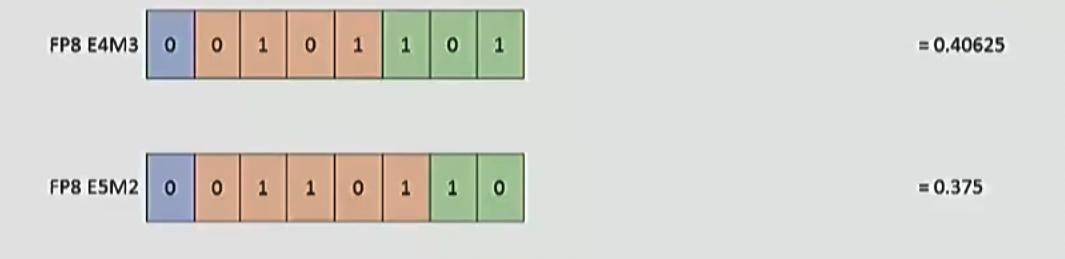
• 英伟达提出, 专为机器学习任务优化
• 占用空间小, 但是失去了很多精度/动态范围

精度选择

• 用 fp32 训练效果好, 但是占用内存大
• 用 fp8, fp16, bfloat16 有一定的不稳定的风险

解决方法: 使用混合精度训练, 为每一个环节设计并指定对应的合适地精度类型

计算统计 Compute accounting

GPU 上的张量 tensors on GPUs

• 默认情况下, 张量被存储在内存(CPU memory)中
• 然而在 CPU 上处理相关计算很慢, 因此需要指定张量移动到 GPU 上

张量运算 tensor operations

• 大多数张量是通过对其他张量执行操作而创建
• 每个计算都会有一定的内存和计算开销

张量存储 tensor storage

• Pytorch 中, 张量是指向内存的指针
• 存储方式其实跟 C 语言里的高维数组很像?

张量切片 tensor slicing

• 许多运算只是变换了同一张量的展现形式

• 因此需要搞清楚一些张量运算到底是在原张量操作, 还是在张量的副本上操作

• 对于 transpose 等操作, 会导致张量不再连续, 因此在 view 的时候需要先使用 contiguous() 方法

张量的按位运算 tensor elementwise

张量矩阵乘法 tensor matmul

tensor einops

我也不知道这个 einops 是啥, 大概是某一个库吧

出现的动机

在 torch 中, 我们常常会对不同维度进行一些操作和运算
然而这相对比较抽象, 记忆每个维度对应的含义也并非易事
因此, 我们引入 einops 方法, 对每个维度对应的含义进行标记, 避免混淆

einops_einsum

einsum 全称是 Einstein Summation（爱因斯坦求和约定），它通过字符串公式定义张量运算，语义清晰、灵活强大，主要用于：

• 张量乘法（内积 / 外积 / 点积 / 矩阵乘法等）
• 转置与重排
• 批量广播计算
• 自动求和（隐式 sum）

1

z = einsum("abc,acd->abd", x, y)

1. 相同字母表示对齐维度
2. 输出中不出现的维度会被求和掉（sum）
3. 不同字母表示保持独立维度

einops_reduce

einops.reduce 是 einops 库中的一个核心函数，用来对张量进行指定维度的聚合运算，比如：

• 求和（sum）
• 求均值（mean）
• 最大值（max）
• 最小值（min）

1
2
3

from einops import reduce

output = reduce(tensor, pattern, reduction)

• tensor：输入的张量（如 PyTorch 的 Tensor）
• pattern：字符串，描述你想保留和聚合的维度
• reduction：字符串，表示使用哪种聚合方式，如 ‘sum’、‘mean’、‘max’

1
2
3
4
5
6
7

import torch
from einops import reduce

x = torch.randn(32, 128, 64)  # [batch, seq_len, hidden]
y = reduce(x, 'b s h -> b h', 'mean')  # 沿 seq_len 聚合

print(y.shape)  # (32, 64)

einops_rearrange

rearrange 的作用是：重排张量维度和形状，相当于 reshape + transpose + unsqueeze + flatten 的组合。

1
2
3

from einops import rearrange

output = rearrange(tensor, pattern)

• tensor：输入张量
• pattern：形状转换模式（字符串），写明你从什么变成什么
• 可选关键词参数：…、维度大小等（有时需要指定形状）

1
2
3

x = torch.randn(10, 3, 4)
y = rearrange(x, 'b c h -> b (c h)')
print(y.shape)  # (10, 12)

张量操作的计算成本 tensor_operations_flops

基本概念

浮点操作(FLOP)是指任何涉及浮点数的操作, 比如加法, 乘法, 等等

易混名词:

• FLOPs: 浮点运算次数, 用于衡量 计算量
• FLOP/s:每秒浮点运算数, 用于衡量硬件能力

直观理解

• 训练 GPT3 需要 3.14e23 FLOPs

• 训练 GPT4 需要 2e25 FLOPs

• A100 峰值算力 312 tera FLOP/s == 312e12 FLOP/s

• H100 峰值算力(稀疏) 1979 tera FLOP/s == 1979e12 FLOP/s

整体而言, 矩阵运算是运算量最大的部分
其中, 对 m x n , n x p 矩阵进行矩阵乘法, 运算量为 2 x m x n x p

Model FLOPs Utilization(模型 FLOPs 利用率)

简称 MFU
它衡量的是：

你训练模型时的实际 FLOPs 占理论最大 FLOPs 的比例
衡量模型是否吃满了算力，是工程和系统优化的关键指标

1

MFU = 实际使用的 FLOPs / 理论最大 FLOPs（由 GPU 理论峰值计算能力决定）

值的范围：

• 0%（啥都没干）
• 100%（理论极限利用）
• 一般以 50% 为界限, 超过则较优

低 MFU 说明：模型小、batch 小、数据加载慢、通信慢、未并行优化等

梯度基础 gradients_basics

计算量中, 还有一部分来自于梯度的计算

模型 Models

参数 parameters

pytorch 中, 参数被存储为 nn.parameter 对象

参数初始化 parameter initialization

为何初始化

在模型运算中, 矩阵乘法输出的数值规模会与隐藏维度的平方根成正比.
因此当模型很大时, 运算结果会很大, 导致梯度爆炸, 训练不稳定
我们需要采用某种方法, 避免这种情况

参数初始化

我们通过对参数进行缩放, 抵消运算带来的数值的放大, 避免过大的运算结果
我们在初始化后, 把所有参数缩放至原先的 1/sqrt(num_inputs) 倍, 用来抵消后续放大的影响
相关的比较成熟的研究, 可以见 Xavier initialization

自定义模型 custom_model

关于随机性 randomness

随机性在模型中时常被用到: 参数初始化, dropout, 数据排序……
为了便于复现, 最好在每次使用时指定随机种子

数据加载 data_loading

语言模型中, 经过 tokenization, 数据变成了一系列整型数字
数据通常很大, 无法一次性全部加载到内存中
可以使用 memmap, 建立数据到内存间的映射关系, 只把需要访问的数据加载到内存上
可以写一个 dataloader, 用于从所有数据中, 多次采样小批量的数据

优化器 optimizer

• momentum = SGD + 对梯度做指数加权平均
  • 让更新方向更平滑，减少梯度震荡
• AdaGrad = SGD + 对梯度平方求累计平均（累积求和再开方）
  • 每个参数都有自己的学习率缩放因子
• RMSProp = AdaGrad + 用指数加权平均
  • 避免学习率快速衰减到 0
• Adam = RMSProp + Momentum
  • 同时维护
  • 一阶矩（梯度的指数加权平均） → 类似 Momentum
  • 二阶矩（梯度平方的指数加权平均） → 类似 RMSProp
  • 还加了偏差修正

训练循环 train_loop

检查点 checkpoint

训模型需要很长时间, 为了防止某时的崩溃导致前功尽弃
采用定时将模型保存到磁盘的方式, 具体保存的内容有: 模型, 优化器, 迭代次数
后续可以加载保存的检查点

我的问题: 为什么要保存优化器?

优化器里不仅有超参数，还存储了训练过程中的状态信息，这些状态会影响后续的梯度更新，如果不保存，就无法无缝恢复训练

混合精度训练 mixed_precision_training

这种训练方法最早在 2017 年被提出
正如之前提到的, 不同的精度类型有自己的优缺点
因此可以根据具体任务类型, 指定精度, 提升效率和效果

• bfloat16, fp8 用于前向传播(激活函数)
• float32 用于其他部分(参数, 梯度)

用低精度训练很难, 但是当训练完后把模型通过量化等方式转换为低精度很简单