课程笔记

【NN Zero to Hero】Makemore - part 3

初始化

../动手学深度学习/4.8 数值稳定性和模型初始化

不合理的随机初始化

当概率相等

回顾上一次的模型, 我们发现第一个 epoch 的 loss 巨大 (27), 但是在第二个 epoch 中便突然下降到 2, 这说明我们的初始化并不合理:
AK 做了一个尝试, 把概率设为 1/27 也就是所有字符等概率出现, 按照此概率计算 loss, 也才 3 出头

调整 W 和 b

这里我们可以为一开始初始化的 W, b 做出调整, 比如乘以 0, 这样一来当我们用 softmax 计算, 得到的就是: 1/27, 1/27, …, 1/27 这样的 list, 也就是等概率
再经过交叉熵计算 loss, 便得到了 3 出头的 loss, 也就是等概率对应的 loss

W 必须非零

最后 AK 把 W 的缩放因子从 0 改成了 0.01，虽然初始 loss 略大于等概率输出，但这是因为 softmax 输出不再完全均匀，交叉熵对偏差更加敏感。但这反而为模型提供了“学习空间”。
我的理解是：当 W 为零时，模型输出稳定，但完全无法学习。相反，b 设置为 0 是一种常见的初始化方法，对训练没有负面影响。

为什么无法学习？

这需要回溯到反向传播的原理：
当 W 被乘以 0 后，其实是被 PyTorch 视为一个新的常量张量，并未挂在原有的计算图上。这导致在反向传播时 W 无法接收到来自 loss 的梯度更新。即使后续人为设置了 requires_grad=True，也无法补救这一点 —— 因为梯度路径已经断开了。

激活函数

激活与梯度

接下来，我们来讨论激活函数 tanh 的行为及其对梯度传播的影响。

进入源代码可以看到 tanh 的计算公式：

$$ \tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1} $$

该函数的导数为：

$$ \frac{d}{dx} \tanh(x) = 1 - \tanh^2(x) $$

从这个公式可以看出：

  • 当 $\tanh(x) \approx \pm1$（输出接近饱和区）时，导数趋近于 0，反向传播时梯度几乎无法传递；
    • 这表示神经元已经“非常确定”，几乎不再学习（梯度 * 0）；
  • 当 $\tanh(x) \approx 0$（输入在线性区）时，导数接近 1，梯度可以完整传递；
    • 此时神经元“未激活”，但更容易被训练（梯度 * 1）
      因此，“激活”指的是正向输出的状态，而不是是否能训练；
      梯度是否能通过，取决于当前激活函数的导数值。

调整 W 和 b

通过可视化每个神经元的激活值分布，可以发现如果使用默认初始化的 W₁ 和 b₁，很多神经元的输出直接落在 tanh 的饱和区（即接近 ±1）。

这会导致：

  • 正向输出看似“激活”，但
  • 反向传播中导数趋近 0，梯度几乎无法更新参数。

因此，我们需要：

  • 缩小权重 W 的初始值（如乘以 0.1）；
  • 缩小偏置 b 的初始值（如乘以 0.01）；
    这样可以使输入集中在 tanh 的线性响应区（输出接近 0），
    从而提升神经元的可训练性，确保梯度能顺利传递。

🧠 小结：

  • Tanh 输出接近 ±1 → 激活强，但梯度小；
  • Tanh 输出接近 0 → 未激活，但梯度大 → 更容易训练；
  • 合理初始化 W 和 b，有助于让神经元进入“容易训练”的区域。

Kaiming 初始化

保持分布情况

神经网络中的数值在每层之间传递时, 其分布情况会发生改变 (比如被分布直方图压缩/被拉伸), 因此我们需要通过观察数据分布, 并调整, 使得每一层输出的方差保持稳定, 避免前向/反向传播中信息被放大/消减
我们可以通过给权重矩阵乘以某个值, 对分布进行缩放, 那么问题来了: 如何确定具体的值呢?

关于 ReLU

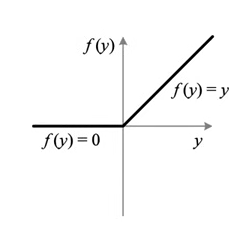
../../source/ReLU function.png
Relu 函数是一个 squashing function (挤压函数)
这是 ReLU 函数的曲线: 所有大于 0 的数正常输出, 所有小于 0 的数被截断为 0
由于丢掉了一半的分布, Kaiming 发现需要用一些 gain (增益) 进行补偿

Gain 增益

Kaiming 发现, 需要在用高斯分布初始化权重矩阵时, 需要乘以一个 gain, 具体大小是: $\sqrt{2/n_l}$
其中: 2 主要是为了弥补 ReLU 函数丢掉的一半对于分布造成的影响, $n_{l}$ 指的是 fan_in, 也就是输出神经元连接的输入数

PyTorch 中的 Kaiming 初始化 

1

torch.nn.init.kaiming_normal_( tensor, a=0, mode='fan_in', nonlinearity='leaky_relu' )

对于不同的非线性激活函数, gain 有着不同的计算方式
在 Kaiming 初始化提出之前, 选择激活函数, 设置相关的 gain 必须十分谨慎, 反复微调. 在给出了每一种激活函数对应的 gain 之后, 大大的便利了初始化的设置.

关于 fan

“fan”其实是从“fan-out / fan-in of a neuron”这类术语中来的，源自电子工程和神经网络的早期研究。

fan 在这里的含义是“扇出”或“扇入”的意思，就像风扇的叶片（fan blade）那样向外/向内展开连接。

神经网络中的用法

  • 每个神经元可能连接很多前一层的输出，这些输入的数量叫 fan-in；
  • 它可能连接很多后一层的神经元，叫 fan-out。

计算方法

举个例子：

1

nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3)
  • fan_in = 3 × 3 × 3 = 27
  • fan_out = 64 × 3 × 3 = 576

Batch Normalization (BN)

通过调整权重矩阵的分布, 提升了模型效果后, 我们进一步想: 能否通过调整每个 mini-batch 中数据的分布, 进一步优化模型? 这种方法便称为 BN, Batch Normalization.

目的

  • 缓解 Internal Covariate Shift（内部协变量偏移）
  • 加速训练，提升稳定性
  • 防止梯度爆炸或消失
  • 允许更大的学习率、更快收敛

计算公式

（以一个神经元维度为例） 设一个 mini-batch 中有 ( m ) 个样本，某一层的某个神经元输出为：
$x_1, x_2, \dots, x_m$

第一步：计算 mini-batch 的均值

$\mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i $

第二步：计算 mini-batch 的方差

$\sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 $

第三步：标准化

$\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$
其中 $\epsilon$ 是一个很小的正数，用于防止除以 0。

第四步 ：缩放和平移（可学习参数）

$ y_i = \gamma \hat{x}_i + \beta$
其中 $\gamma$ 和 $\beta$ 是可学习参数，恢复网络的表达能力。
这其实也是算作一种对于改变 batch 中数据原始分布而做出的一些"补偿", 让模型可以自己调整表达能力

注意: BN 用于数据进入激活函数之前, 使得不要让神经元被激活得太“过火”或“失联”，而是尽量保持输入分布稳定，均值为 0，方差为 1，让激活函数处于“有效工作区间”

推理时的 BN

刚才的 BN 其实是针对训练时的每一个 Batch, 然而在推理时, 输入的数据很少, 如果仅仅把输入数据作为 mini-batch 来进行 BN 的话, 会有很大的误差, 所以我们需要尝试其他的方法

全局 BN

我们可以采用在整个数据集上计算 bn 相关值, 由于后续推理时进行 BN:

1
2
3
4
5
6
7
8
9

# calibrate the batch norm at the end of training
with torch.no_grad():
  # pass the training set through
  emb = C[Xtr]
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 # + b1
  # measure the mean/std over the entire training set
  bnmean = hpreact.mean(0, keepdim=True)
  bnstd = hpreact.std(0, keepdim=True)

这里不记录梯度, 因为不需要构建计算图用于反向传播中更新参数, 只是单独的计算而已
这里是对整个数据集进行 mean 和 std 的操作

另一种近似全局 BN 的方法

我们可以根据每个 minibatch 的数据, 迭代更新 mean 和 std, 得到和全局 BN 极其近似的值, 可以平替, 能够节省计算资源

初始化

可以在初始化的时候设置好 bn 相关的变量, 用于后续计算和更新

1
2
3
4
5

# BatchNorm parameters
bngain = torch.ones((1, n_hidden))
bnbias = torch.zeros((1, n_hidden))
bnmean_running = torch.zeros((1, n_hidden))
bnstd_running = torch.ones((1, n_hidden))

这里的 bngain 和 bnbias 是作为变量, 参与后续反向传播的更新的
mean 和 std 在这里是running, 是随着每个 batch 的遍历进行更新, 在初始化时分别使用 zeros 和 ones 的方法

mini-batch 中的更新 

1
2
3
4
5
6

bnmeani = hpreact.mean(0, keepdim=True)
bnstdi = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
with torch.no_grad():
	bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
	bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi

这是在遍历每个 minibatch 时的代码, 这里的 meani 和 stdi 是指的当前 batch 的 bn 相关的值, 然后根据公式计算出 hpreact
同时, 打开 nograd, 因为这里的计算不需要记录计算图用于反向传播
在标准的 Batch Normalization 训练流程中，每次用当前 mini-batch 的均值和方差做归一化，但同时我们也维护一个“滑动平均”的全局统计量
这就是所谓的 exponential moving average（EMA），其目的是：

累积多个 batch 的统计量，作为推理时的稳定估计。

多余的 bias

通过观察代码和公式, 我们可以发现

1
2
3
4
5
6
7

# Linear layer
hpreact = embcat @ W1 #+ b1 # hidden layer pre-activation
# BatchNorm layer
# -------------------------------------------------------------
bnmeani = hpreact.mean(0, keepdim=True)
bnstdi = hpreact.std(0, keepdim=True)
hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias

原有的这个 b1, 在经过 mean, 并做差想减后, 正好抵消了
因此它并不会在计算图中出现, 进而不会在反向传播中更新值, 所以这个 b1 根本没有必要
进一步, 所有 BN 层都不需要原本的 bias

那谁来发挥 bias 的作用 ?

这是我一开始的疑惑, 与 gpt 交流后得到了解答:
因为 BN 层中其实有 bnbias, 且是参数, 可以在后续被更新, 相当于发挥了原本线性层中 bias 的作用

comments powered by Disqus
© 2024 - 2025 Haoqing
使用 Hugo 构建
主题 Stack 由 Jimmy 设计