PageRank - CS50’s Introduction to Artificial Intelligence with Python
这里是要做一个页面排序的程序,前言中提到了一些算法
transition model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
def transition_model(corpus, page, damping_factor):
"""
Return a probability distribution over which page to visit next,
given a current page.
With probability `damping_factor`, choose a link at random
linked to by `page`. With probability `1 - damping_factor`, choose
a link at random chosen from all pages in the corpus.
"""
dic = {}
d = damping_factor
links = corpus[page] #获取当前 page 上的所有链接
if len(links) == 0:
links = corpus.key() #如果当前页面上没有任何链接,则跳转范围是所有页面
num_links = len(links)
num_pages = len(corpus)
for p in corpus: #对所有页面进行遍历
if p in links: #如果该页面位于当前page的链接之中
dic[p] = (1 - d) / num_pages + d / num_links
else:
dic[p] = (1 - d) / num_pages
return dic
|
这里主要是做一个转移模型,用于表示从当前页面 page 到其他页面的概率
返回值是一个字典,每个页面与对应的跳转概率绑定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
def sample_pagerank(corpus, damping_factor, n):
"""
Return PageRank values for each page by sampling `n` pages
according to transition model, starting with a page at random.
Return a dictionary where keys are page names, and values are
their estimated PageRank value (a value between 0 and 1). All
PageRank values should sum to 1.
"""
current_page = random.choice(list(corpus.keys())) #第一个页面从所有页面中随机选取
visits = {page : 0 for page in corpus} #新建一个字典,用于存储访问次数
for _ in range(n): #循环n次
transition_probability = transition_model(corpus,current_page,damping_factor) #调用模型,获取在一个页面的分布情况
next_page = random.choices(population=list(transition_probability.keys()),
weights=list(transition_probability.values()),
k = 1)[0]
#调用random函数,进行加权的随机跳转
current_page = next_page #更新当前页面
visits[current_page] += 1 #更新访问次数
total_visits = sum(visits.values())
ranks = {page: visits[page] / total_visits for page in list(corpus.keys())}
return ranks
|
这里是要进行采样,获得一个模拟的概率,作为 pagerank 进行返回
需要注意的是:
- 这里的 keys、values 等方法返回的似乎是一个 iter 的东西,需要用 list 转换一下
- random 函数中方法的选用,注意返回的是数还是列表
- 一些字典的小窍门,具体请看代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
def iterate_pagerank(corpus, damping_factor):
"""
Return PageRank values for each page by iteratively updating
PageRank values until convergence.
Return a dictionary where keys are page names, and values are
their estimated PageRank value (a value between 0 and 1). All
PageRank values should sum to 1.
"""
d = damping_factor #阻尼系数
N = len(list(corpus.keys())) #总页面数
rank = {page : 1 / N for page in corpus} #给每个页面的 rank 初始赋值
while True:
max_change = 0 #初始化最大改变量
new_rank = {} #新的rank字典,用于记录后统一更新
for page in corpus: #开始遍历每一个page
page_rank = (1-d)/N #初始的 pagerank,剩余部分需要分类讨论
for other in corpus: #再进行一个遍历,用于找出含有指向 page 的链接的 other
if page in corpus[other]: #如果page在链接之中,套公式计算
page_rank += d*rank[other]/len(corpus[other])
elif not corpus[other]: #如果该other页面没有出口的链接,则视为有指向所有页面的链接
page_rank += d*rank[other]/N
max_change = max(abs(page_rank - rank[page]),max_change) #每次更新记录最大改变
new_rank[page] = page_rank #存到新的rank 字典中
rank = new_rank #循环后为字典统一赋值
if max_change <= 0.001: #判断是否可以终止
break
return rank #返回最终的rank
|
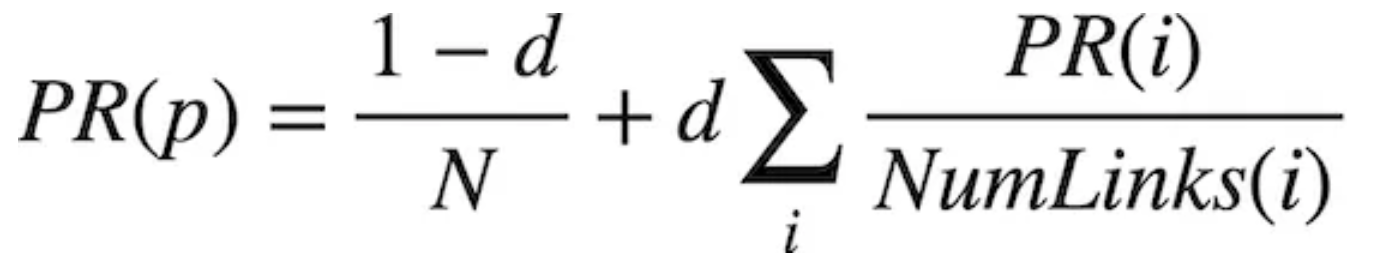
这里需要使用这个公式进行计算,具体细节用注释写的已经比较清楚了
这里主要是通过不断更新,达到一个稳态,把稳态的结果作为最终 pagerank 的拟合值

到此,pagerank 完结