线性分类器
流程
- 展开图像
- 矩阵乘法:每一行的权重矩阵对应着每一个类别的"打分规则"
- 加上偏置
- 得到 logits
- 转化为概率
线性的预测
由于矩阵乘法的特性, 可以把对图像像素的缩放系数提取
我们发现, 对于图像像素值的缩放, 等价于对预测的 logits 的缩放
$$
f(c*x,W) = W(c*x) = c*f(x,W)
$$
理解线性分类器
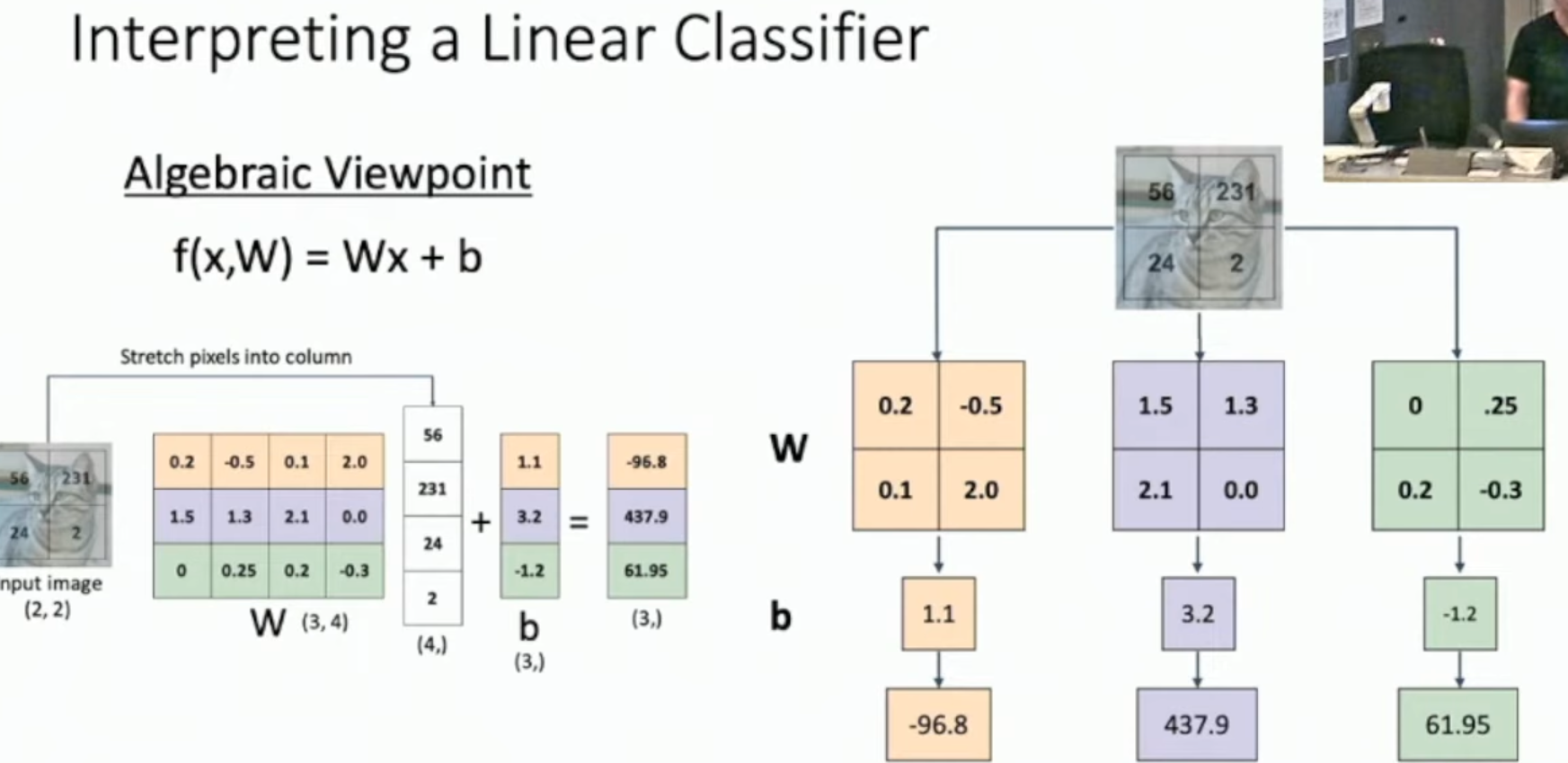
模板匹配
把展开的图片复原, 并将权重矩阵 reshape 成图片的形状, 这可以被形象地理解为"模板匹配"
分离器的局限
视觉角度
线性分离器中, 每一类只能学到一个模板
它会将现实中同一物体/物种的不同形态学习, 得到一个"平均"的物体
(比如一只有两个头的马)
几何角度
几何意义上, 这一个模板, 对应的参数矩阵, 可以在高维坐标系上绘制出一条决策边界, 决策边界是一条直线或者一个超平面
因此, 其无发刻画一些复杂的情形, 仅能处理一些简单任务
损失函数
多类 SVM 损失
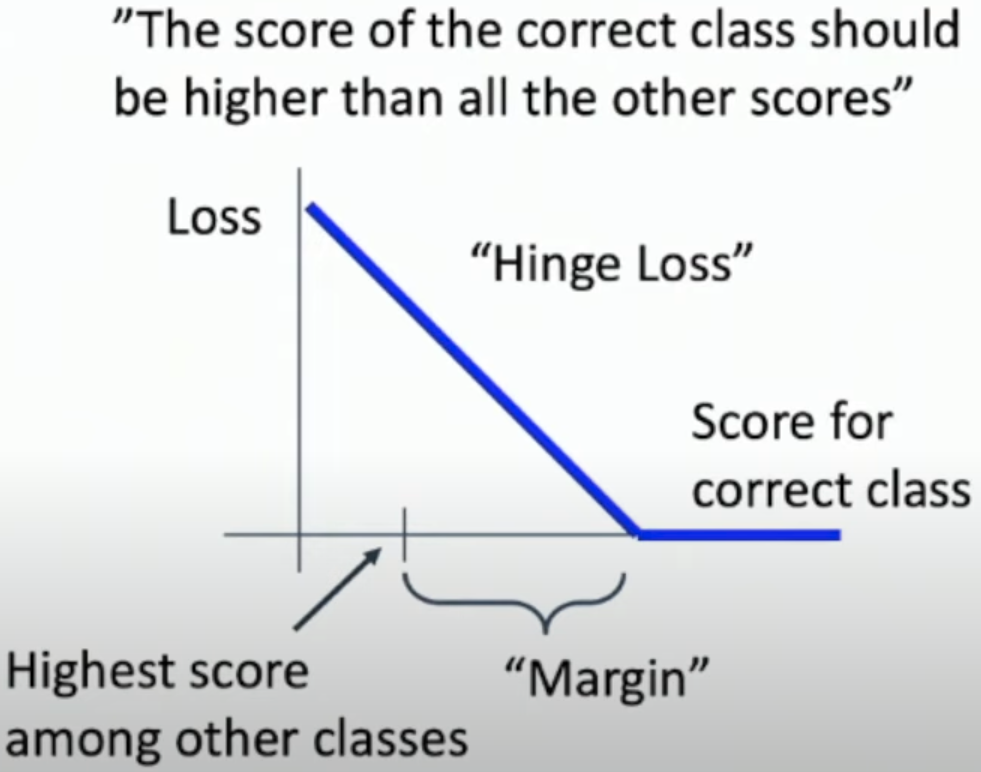
- 当正确类别得分还没有高出其他类别足够 margin 时,损失随着得分增加而线性降低
- 当正确类别得分超过 margin 后,损失为 0
交叉熵损失 Cross-Entropy Loss
softmax
交叉熵损失主要应用在概率上, 因此需要先将各种 logits 转换为概率分布
softmax 已经讲过很多遍了, 就是把 logits 取 exp, 然后进行归一化, 得到概率分布
交叉熵损失
$$
L_i = -logP(Y=y_{i} \mid X=x_{i})
$$
和 softmax相结合, 也就是
$$
L_{i} = -log(\frac{e^s_{y_{i}}}{\sum_{j}e^s_{j}})
$$
正则化
作用
避免模型在训练集上表现太好, 导致过拟合. 正则化项会加在损失函数上, 增强模型的泛化能力
简单方法
L1 正则化
$$
R(W) = \sum_{k} \sum_{L} \mid W_{k,l}\mid
$$
促进稀疏(让部分权重趋近于零), 有助于特征选择
L2 正则化
$$
R(W) = \sum_{k} \sum_{L} (W_{k,l})^2
$$
让权重尽量小但不强制为零,鼓励平滑的模型
Elastic Net
其实就是 L1 和 L2 的组合
$$
R(W) = \sum_{k} \sum_{L} \mid W_{k,l}\mid + \beta W^2_{k,l}
$$
同时兼顾 L1 稀疏性和 L2 平滑性
其他方法
- Dropout
- Batch Norm