原始梯度下降

• 每次按照 负梯度方向（最速下降方向） 走一点点，逐步减小损失函数

超参数

1. 权重初始化
2. 迭代次数
3. 学习率

随机梯度下降 SGD

损失函数

在 N 很大时, 全量求和太慢
因此随机选一个 minibatch, 用每个 minibatch 来近似全局梯度.
这样的多次小批量近似梯度下降比全量梯度下降效率更高

超参数

1. 权重初始化方式
2. 迭代步数
3. 学习率
4. 批量大小
5. 抽样方式

问题

1. 在平缓的位置变化缓慢, 在陡峭的位置剧烈变化
2. 会困在局部最小值, 无法继续迭代更新
3. minibatch 会带来梯度噪声

动量 momentum

如果把梯度下降的过程类比成小球下坡, 那动量的引入就是让小球拥有惯性
可以防止路径过度震荡, 帮助 loss 更快更稳定地收敛
同时, 前面积累的动量/速度也可以帮助小球越过局部最低点, 防止卡住

Nesterov Momentum

• 先沿着动量方向提前看一步
• 在”预期到达的位置”计算梯度
• 再用这个“更精准的梯度”更新

自适应梯度 AdaGrad

核心思想

每个参数有自己的学习率，并且 会随着训练自动调整（自适应）
关键机制：

• 对每个参数，累计历史梯度平方和
• 梯度越大，学习率衰减得越快 — 避免震荡
• 梯度越小，学习率衰减得慢 — 加快收敛

细节

1
2
3
4
5

grad_squared = 0
for t in range(num_steps):
    dw = compute_gradient(w)  # 计算当前梯度
    grad_squared += dw * dw   # 梯度平方累加
    w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)  # 参数更新

• 累加所有历史梯度的平方
• 问题：历史累计不会消失，导致学习率持续衰减，最终趋近于零，更新步长越来越小

RMSProp

“Leaky AdaGrad”
由于 AdaGrad 会导致学习率持续衰减, 最终趋于零
RMSProp 根据这个问题做出了一些改进:

• 引入了衰减率
• 每次只保留部分历史信息，其余部分被“遗忘”

Adam

RMSProp + Momentum
Adam 同时维护：

• 一阶矩（moment1）：梯度的指数加权平均 → 类似 Momentum
• 二阶矩（moment2）：梯度平方的指数加权平均 → 类似 RMSProp

1
2
3

moment1 = beta1 * moment1 + (1 - beta1) * dw # 类似 Momentum 
moment2 = beta2 * moment2 + (1 - beta2) * dw * dw # 类似 RMSProp 
w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)

• 自适应学习率：每个参数有独立学习率
• 动量加速：方向更平滑，不易震荡
• 无需手动调整学习率衰减，鲁棒性强

Adam 在实际中非常常用

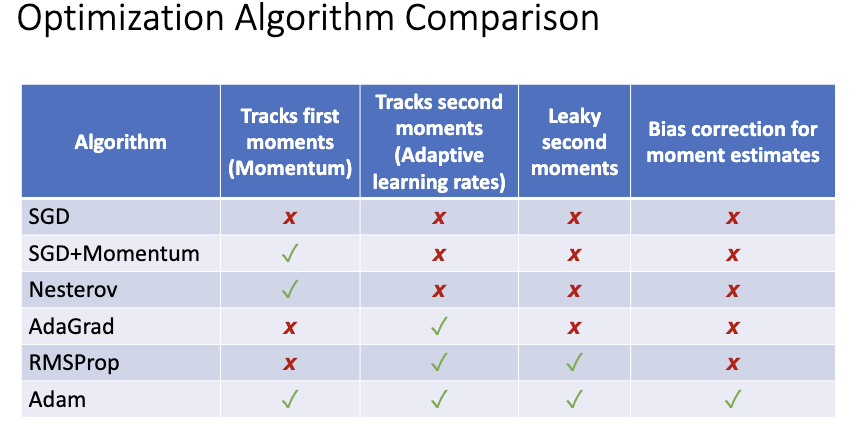
优化方法对比

AdamW

传统 Adam + L2 正则化

• 把正则项加在 loss 里，直接影响梯度计算
• 缺点：对于自适应优化器（如 Adam），正则项会被梯度缩放影响，导致衰减效果被扭曲

AdamW 思想

• Decoupled Weight Decay（解耦权重衰减）：
• 不再把权重衰减加到 loss 里，而是直接在参数更新时手动衰减参数，独立于梯度计算，衰减效果更准确

AdamW 优点：

• 衰减更稳定，收敛更快
• 泛化能力更强，适合深度学习（尤其 Transformer、BERT 等模型）

一阶优化与二阶优化

一阶优化

• 只用 梯度（Gradient） 来近似损失函数的线性变化
• 每一步的更新方向就是 梯度反方向，步长由学习率控制
  优点:
• 计算简单，代价低
  缺点:
• 容易震荡，步长不自适应，可能收敛慢

二阶优化

• 使用 梯度 + Hessian（海森矩阵，二阶导数） 做二次近似

• 一阶方法只知道“坡有多陡”

• 二阶方法还知道“坡是凸的还是凹的”

• 但是计算量非常大

小总结

• Adam是一个不错的默认选择
• SGD + Momentum 可以表现更好, 但是需要很多时间去微调